|
contents:
Engl
|
Calculation of moving of the center of mass of the closed mechanical system is executed on the basis of a principle of conservation of momentum and by means of Lagrange's equations.
In time
In a Fig. 8 plots of change of momentums for the working period are presented: systems of moving elements that reduce their weight:
and the body of the device that increases its weight:
The
plot of a total momentum, i.e. linear momentum of all system,
coincides with an axis of abscissas the plot.
Fig. 8 It is possible to speak only about conditional speed and conditional acceleration of the center of mass of all mechanical system for the working period. Speed of system is a derivative on time from coordinate. Let's leave while in the party calculation on one of coordinates. Below it will be explained, in this connection it is connected.
The
greatest interest represents change of coordinate
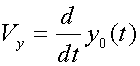
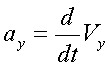
It is protected by the legislation
of the Russian Federation under copyrights.
No part of a site can be reproduced in any form and any means without the written sanction of the owner of copyrights.
// // |