Расчет перемещения центра масс замкнутой механической системы выполнен на основании закона сохранения импульса и с помощью уравнений Лагранжа II рода.

 

За время рабочего периода Т  ( ) суммарный импульс системы равен нулю (Рис. 8). 

Перемещение всей замкнутой системы возникает только во время рабочего периода.

На Рис. 8 представлены графики изменения импульсов за рабочий период:

 системы подвижных элементов —

и «неподвижной», корпуса —

График суммарного импульса, т.е. количества движения всей системы, совпадает с осью абсцисс графика.

Если в любой момент времени остановить относительное перемещение системы подвижных элементов, вся механическая система будет иметь начальную скорость.

Если в начальный момент времени вся механическая система имела нулевую скорость в системе , то после остановки системы подвижных элементов скорость всей механической системы также будет равняться нулю!

 

Рис. 8

Можно говорить только об условной скорости и условном ускорении центра масс всей механической системы за рабочий период.

Скорость системы есть производная по времени от координаты.

Оставим пока в стороне расчет по одной из координат. Ниже будет пояснено, в связи с чем это связано.

Наибольший интерес представляет изменение координаты   (25) или (31).

(34)

 

 

(35)

 

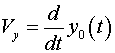
Соответствующие графики изменения "скорости" и "ускорения" всей замкнутой механической системы представлены на Рис. 9 и Рис. 10

Рис. 9

Рис. 10