|
О возможности безопорного перемещения
 2.
Статья 2.
Статья
 2.2.
Анализ движения замкнутой механической
системы, исходя из закона сохранения импульса 2.2.
Анализ движения замкнутой механической
системы, исходя из закона сохранения импульса
 1 2
1 2


 2.2.2. Расчет
количества движения замкнутой механической системы тел в
абсолютной системе координат за рабочий период
Количество движения всей материальной
системы, изображенной на Рис. 1:

|
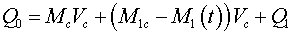
|
(13)
|
Здесь:
 —
количество движения всей замкнутой системы, состоящей из тела —
количество движения всей замкнутой системы, состоящей из тела
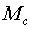 и системы подвижных элементов общей массой
и системы подвижных элементов общей массой
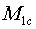
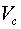 —
скорость центра масс тела
—
скорость центра масс тела
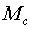 с присоединившимися элементами
с присоединившимися элементами
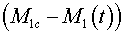 . .
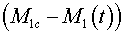 — масса части подвижных элементов, не участвующих в движении по
окружности радиуса
R.
— масса части подвижных элементов, не участвующих в движении по
окружности радиуса
R.
Остановившись в точке
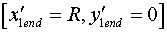 ,
эти элементы приобретают скорость тела ,
эти элементы приобретают скорость тела
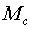 .
(Из условия задачи.) .
(Из условия задачи.)
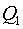 —
количество движения системы подвижных элементов. Проекции —
количество движения системы подвижных элементов. Проекции
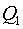 на оси координат найдены выше:
(11), (12).
на оси координат найдены выше:
(11), (12).
Как известно,
центром масс материальной системы называется геометрическая точка, радиус-вектор
r
которой определяется равенством
|
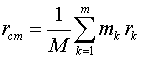 |
(14) |
Поскольку за рабочий период к телу
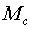 присоединяются дополнительные частицы, координаты центра масс тела
присоединяются дополнительные частицы, координаты центра масс тела
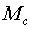 рассчитываются
следующим образом: рассчитываются
следующим образом:
|
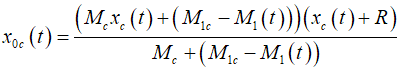
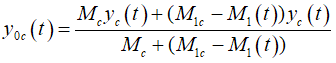 |
(15)
|
где
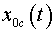 и и
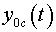 —
координаты центра масс тела —
координаты центра масс тела
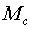 в
системе координат
XOY. в
системе координат
XOY.
После подстановки
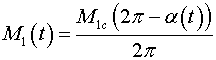 и
и
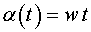 , ,
получим:
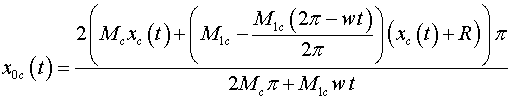
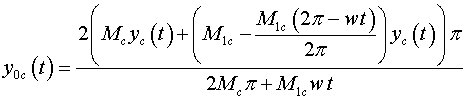
Проекции скоростей на соответствующие оси
координат:
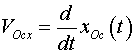
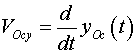
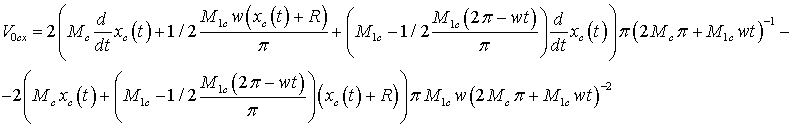
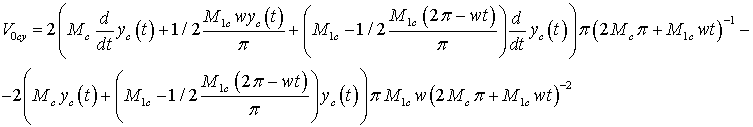
или, после упрощения:
|
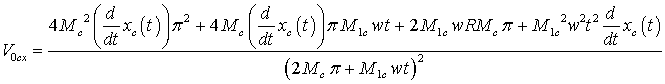
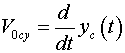
|
(16)
|
В проекции на оси системы координат
XOY
количество движения
 (из (13)):
(из (13)):
|
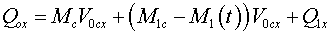
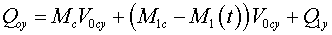
|
(17) |
В соответствии с законом сохранения количества
движения замкнутой системы:
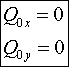

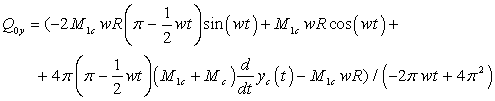
Решение данной системы
дифференциальных уравнений
относительно координат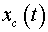 и и
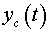 (координат центра масс корпуса), с учетом начальных условий: (координат центра масс корпуса), с учетом начальных условий:
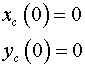
дает следующие результаты:
|
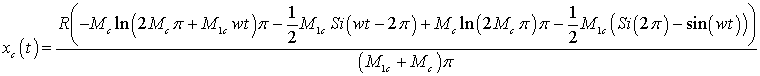
|
(18)
|
|
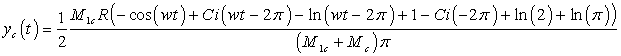
|
(19)
|
, где:
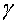 — константа Эйлера:
— константа Эйлера:
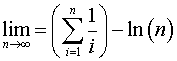 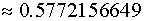
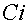 – косинусный интеграл:
– косинусный интеграл:
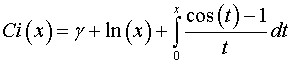
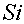 – синусный интеграл:
– синусный интеграл:
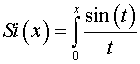
На Рис. 4 представлен график изменения
координат
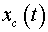 и и
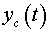 за рабочий период.
за рабочий период.
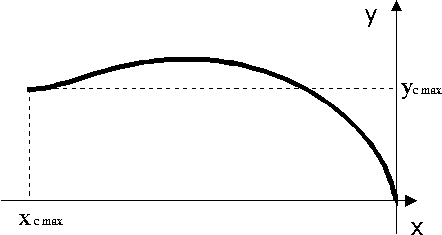
Рис. 4
Еще раз напомним, что
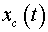 и и
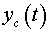 — координаты центра масс тела
— координаты центра масс тела
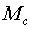 в системе координат
XOY,
т.е. в «абсолютной» системе координат.
в системе координат
XOY,
т.е. в «абсолютной» системе координат.
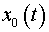 и и
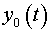 — координаты центра масс всей замкнутой механической системы в
системе координат
XOY.
— координаты центра масс всей замкнутой механической системы в
системе координат
XOY.
Величины
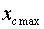 и и
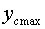 можно найти следующим образом:
можно найти следующим образом:
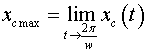
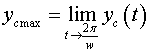
|
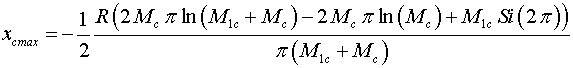
|
(20)
|
|
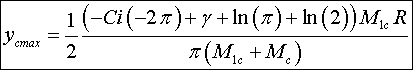
|
(21)
|
Выражение
|
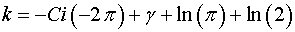 |
(22)
|
есть величина постоянная.
С точностью до 9 знака значение коэффициента
k
составляет: k=2.437653393
|
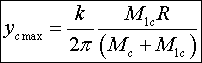
|
(23)
|
|
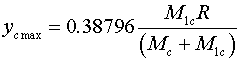 |
(24) |
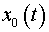 и и
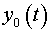 — координаты центра масс всей замкнутой механической системы в
системе координат
XOY.
— координаты центра масс всей замкнутой механической системы в
системе координат
XOY.
Перемещение центра масс всей системы тел
имеет вид (Рис. 5) :
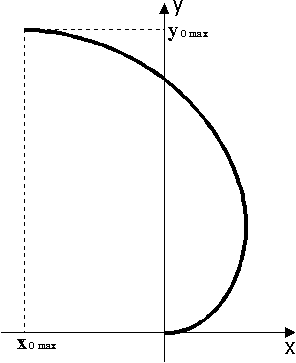
Рис. 5
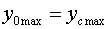
|
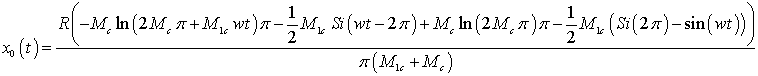 |
(25)
|
|
 |
(26)
|
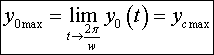
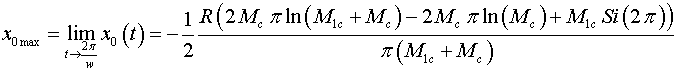
Зависимость перемещения центра масс всей
замкнутой системы представлены на Рис. 6 и Рис. 7 .
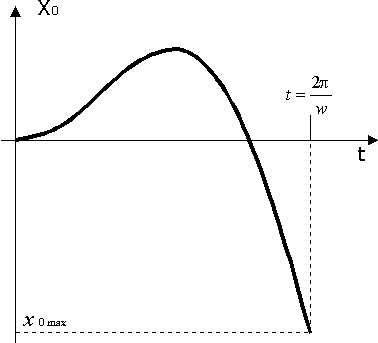
Рис. 6
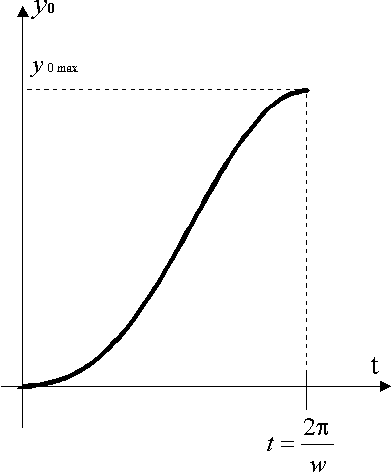
Рис. 7
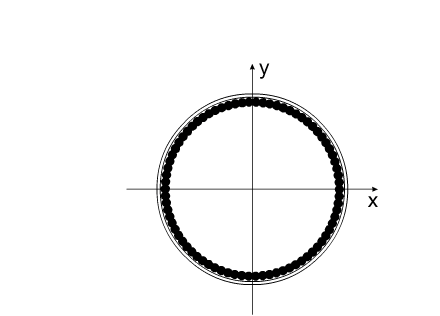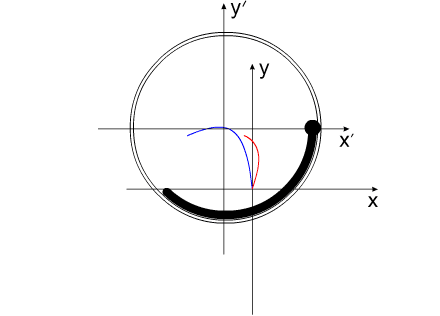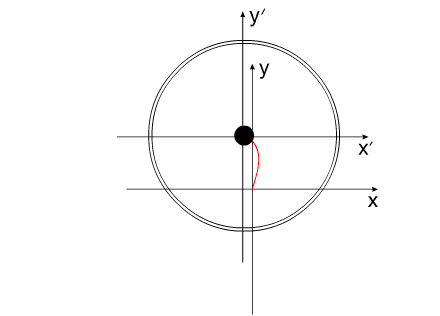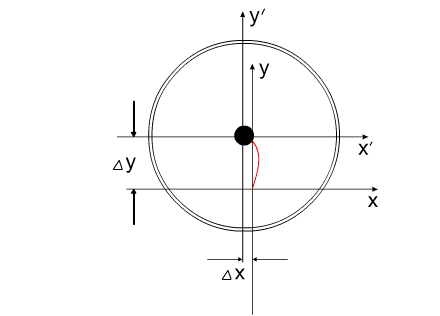
Два графика, представленные на
Рис.4 и Рис.5 , объеденные
в один график:
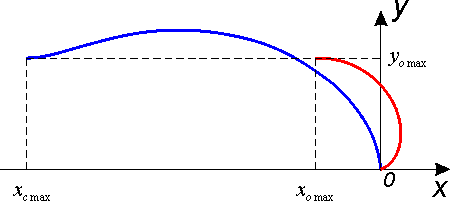
Красным цветом обозначена траектория
перемещения центра масс всей системы
(x0(t)
, y0(t))
(25)(26),
синим - перемещение корпуса
(xc(t)
, yc(t) )
(18)(19).
Выводы.
При условии сохранения импульса данная
система (Рис. 1) перемещается за
определенный промежуток времени на определенное расстояние (Рис.
5).
Оглавление
© ButovSV 07/10/2006
Защищено
законодательством Российской Федерации по авторским правам.
Никакая часть сайта не может быть воспроизведена в какой бы то ни
было форме и какими бы то ни было средствами без письменного разрешения
владельца авторских прав.
Заявка на изобретение №2006134543
|