|
 2.2.2.
Calculation of
a linear momentum of the closed mechanical system of bodies in absolute
coordinates system for the working period
Linear
momentum of all material system represented in
a Fig. 1:
|
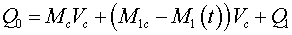
|
(13)
|
Here:
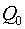 - a linear momentum of all closed system consisting of a body
- a linear momentum of all closed system consisting of a body 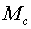 and systems of mobile elements a lump
and systems of mobile elements a lump 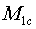
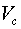 - speed of the center of mass of a body
- speed of the center of mass of a body 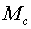 with the joined elements
with the joined elements 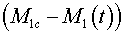 . .
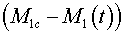 -mass of a part of the mobile elements which are not participating in
movement on a circle of radius
R.
-mass of a part of the mobile elements which are not participating in
movement on a circle of radius
R.
Having stopped in a point 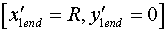 ,
these elements get speed of a body ,
these elements get speed of a body 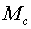 .
(From a condition of a task.) .
(From a condition of a task.)
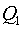 -a linear momentum of system of mobile elements. Projections
-a linear momentum of system of mobile elements. Projections
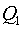 on an axis of coordinates are found above:(11),
(12).
on an axis of coordinates are found above:(11),
(12).
As is known,
the geometrical point, radius-vector
r which
refers to as the center of mass of material system is defined by equality
|
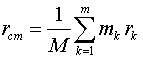 |
(14) |
As for the working period to a body
 additional particles, coordinates of the center of mass of a body join
additional particles, coordinates of the center of mass of a body join
 pay
off as follows: pay
off as follows:
|
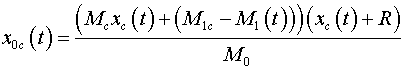
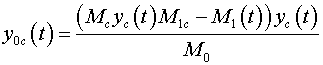 |
(15)
|
where 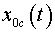 and and
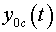 coordinates of the center of mass of a body
coordinates of the center of mass of a body 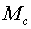 in
coordinate system XOY. in
coordinate system XOY.
After substitution
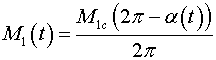 and and
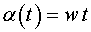 , ,
let's receive:
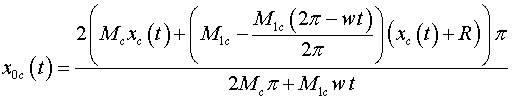
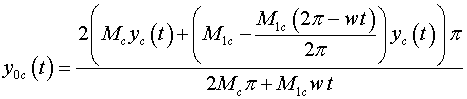
Projections of speeds to corresponding
axes of coordinates:
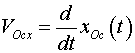
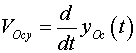
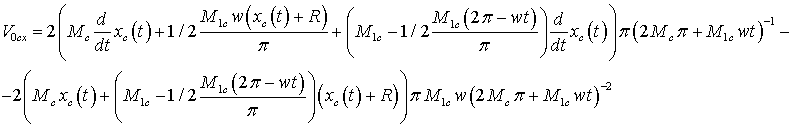
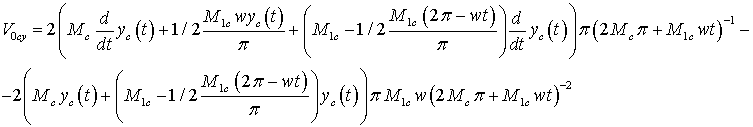
or, after simplification:
|
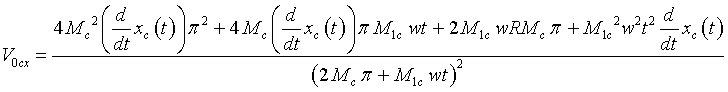 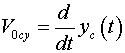
|
(16)
|
In a projection to axes of coordinates
system XOY a
linear momentum 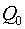 (from(13)):
(from(13)):
|
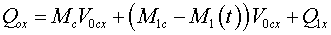
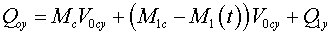
|
(17) |
According to a principle of conservation
of momentum of the closed system:
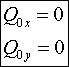
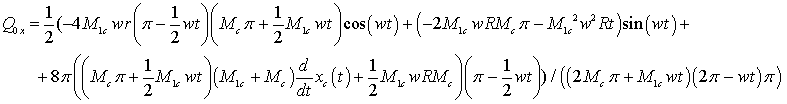
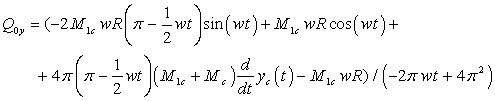
The decision of the given system of the
differential equations concerning coordinates 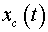 and and
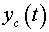 (coordinates of the center of mass of the case), in view
of entry conditions:
(coordinates of the center of mass of the case), in view
of entry conditions:
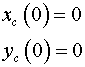
yields following results:
|
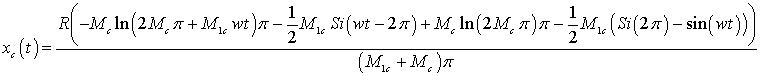
|
(18)
|
|
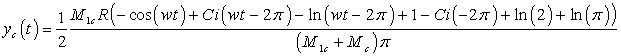
|
(19)
|
, where:
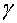 Euler's constant:
Euler's constant: 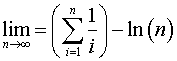 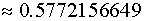
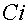 Cosine integral:
Cosine integral:
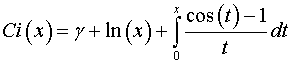
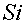 Sine integral:
Sine integral:
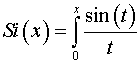
In a Fig. 4 the plot of change of coordinates
is presented 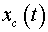 and and
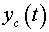 for the working period.
for the working period.
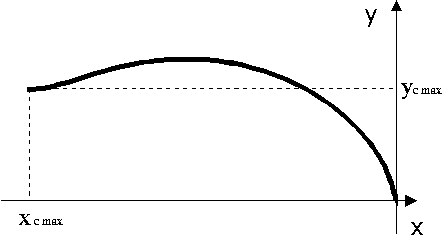
Fig. 4
Once again we shall remind, that 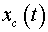 and and
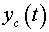 Coordinates of the center of mass of a body
Coordinates of the center of mass of a body
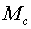 in coordinates system XOY, i.e.
in "absolute" coordinates system.
in coordinates system XOY, i.e.
in "absolute" coordinates system.
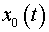 and
and
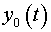 coordinates of the center of mass of all closed mechanical system
in coordinates system XOY.
coordinates of the center of mass of all closed mechanical system
in coordinates system XOY.
values
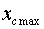 and
and
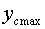 it is possible to find as follows:
it is possible to find as follows:
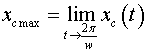
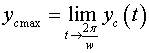
|
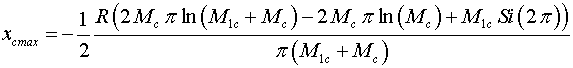
|
(20)
|
|
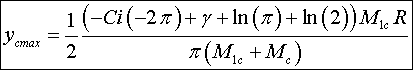
|
(21)
|
Expression
|
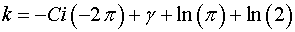
|
(22)
|
there is a size a constant.
To within 9 signs value of factor
k
makes: k=2.437653393
|
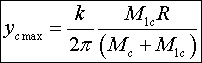
|
(23)
|
|
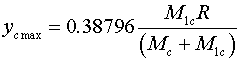
|
(24)
|
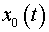 and
and
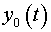 coordinates of the center of mass of all closed
mechanical system in coordinates system XOY.
coordinates of the center of mass of all closed
mechanical system in coordinates system XOY.
With coordinate
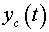 the center of mass of all system
(16) coincides
also.
the center of mass of all system
(16) coincides
also.
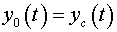
Moving of the center of mass of all
system of bodies looks like (Fig. 5):
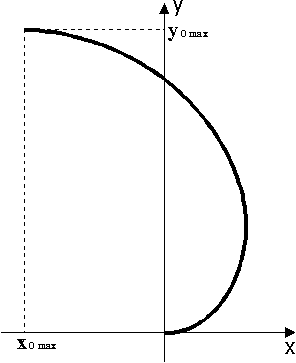
Fig.
5
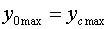
|
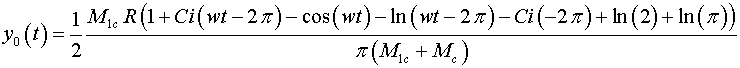
|
(25)
|
|
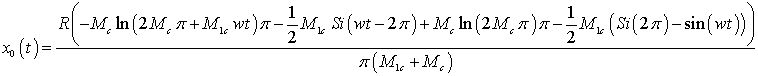 |
(26)
|
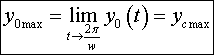
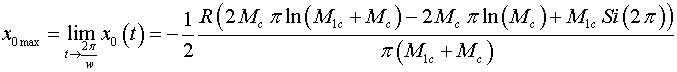
Dependence of moving of the center
of mass of all closed system are presented in a Fig. 6 and a Fig.
7.
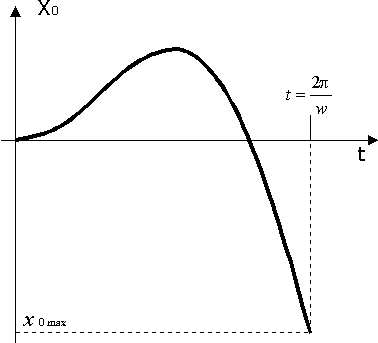
Fig.
6
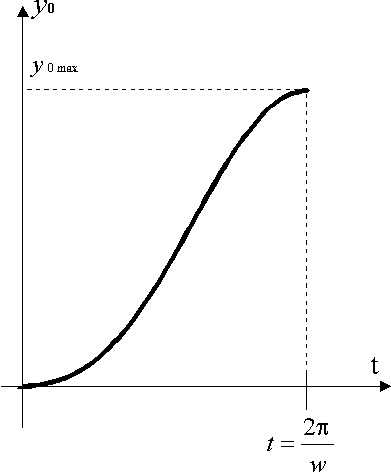
Fig.
7
Two
plots presented on Fig.4 and
Fig 5, collected in
one plot:
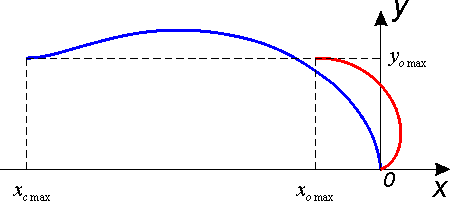
Red color designates a trajectory
of moving of the center of mass of all system, dark blue - moving
of the case (Mc).
Conclusions.
At
observance
condition
of preservation of a momentum the given system (
Fig. 1) moves for the certain
time interval on the certain distance ( Fig. 5).
|