Процесс перемещения рассмотренной системы можно повторить.

Для этого требуется переместить массу M1c , которая собирается на расстоянии R от центра масс Mc, в центр масс Mc.
Не нарушая положения центра масс корпуса, равномерно рассредоточить систему подвижных элементов M1c по окружности радиуса R .
Придать системе подвижных элементов угловую скорость . После этого, рабочий цикл можно повторить (Рис. 25,Рис. 26).

Для того чтобы исключить из расчетов координату  и (где — угол поворота всей механической системы), удобно внести в замкнутую механическую систему еще одну систему подвижных элементов, совершающих движение, зеркально симметричное первой системе подвижных элементов относительно оси .

Рис. 13

 

 

Рис. 14

Под зеркальной симметрией движения подразумевается :

стартовый угол                 

угловая скорость    

изменение массы подвижных элементов 

 

элементы подвижной системы останавливаются в точке с координатами 

 

Координаты центра масс второй подвижной системы

В проекции на оси системы координат  X’O’Y’ количество движения

:

Суммарный импульс систем подвижных элементов в проекции на ось равен нулю.

Суммарный импульс двух систем подвижных элементов в проекции на ось равен удвоенному импульсу одной из систем подвижных элементов.

Сумма моментов импульсов двух систем подвижных элементов равна нулю

Как уже упоминалось выше (Рис. 3), перемещение центра масс системы подвижных элементов в системе координат X’O’Y’ можно сравнить с перемещением центра масс маятника переменной длины и переменной массы . 

Для случая двух систем подвижных элементов, перемещение их общего центра масс можно представить как возвратно-поступательное движение тела переменной массы по одной координате. (Рис. 15).

То есть, механическая система, состоящая из двух систем подвижных элементов, обладает одной степенью свободы.

Рис. 15

 

Анимированное изображение Рис.15:

В течение первого полупериода происходит уменьшение массы двух систем подвижных элементов. При этом координата (центр масс систем подвижных элементов) уменьшается.

В течение второго полупериода , координата возрастает, но масса продолжает уменьшаться до нулевого значения.
 

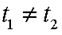Следует обратить внимание:  (см. Рис.8)