Содержание:
Rus
Для замкнутой системы, т. е.
системы, не испытывающей внешних воздействий, или в случае,
когда геометрическая сумма действующих на систему внешних сил
равна нулю, имеет место закон сохранения количества движения.
При этом количество движения отдельных частей системы (например,
под действием внутренних сил) могут изменяться, но так, что
величина 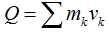 остаётся постоянной.
остаётся постоянной.
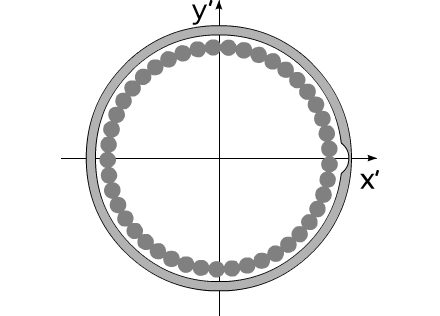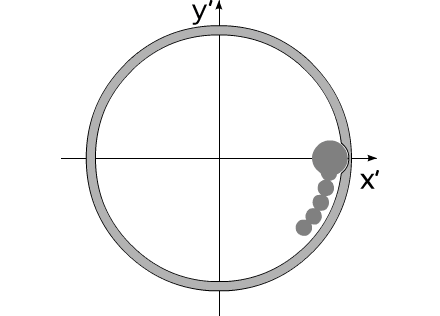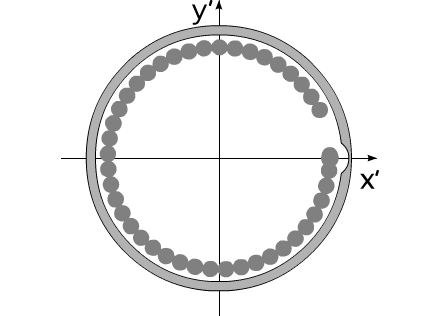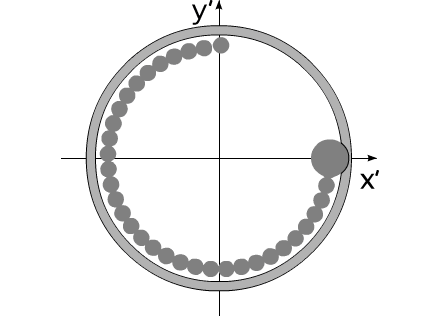
Рассмотрим следующую задачу (Рис. 1):
Рис. 1
Вокруг центра масс массивного тела
Mc, по окружности радиуса
R перемещается с постоянной скоростью система тел суммарной
массой M1c.
Система тел распределена
непрерывно и равномерно. Траектория движения системы тел жестко
связана с телом
Mc.
Перемещение этой системы тел можно
рассматривать, как вращение тела с массой
M1c с постоянной угловой скоростью
w относительно некоторого центра. Предположим, для
упрощения, что каждый элемент
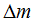 имеет бесконечно малые
геометрические размеры.
имеет бесконечно малые
геометрические размеры.
В определенный момент времени
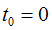 «цепочка» тел
разрывается. Каждый элемент системы начинает останавливается в
точке с координатами
«цепочка» тел
разрывается. Каждый элемент системы начинает останавливается в
точке с координатами
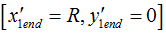 . Остановку
отдельных элементов рассматриваем, как неупругий удар, после
которого элементы приобретают скорость тела
Mc.
. Остановку
отдельных элементов рассматриваем, как неупругий удар, после
которого элементы приобретают скорость тела
Mc.
Остальные тела системы продолжают двигаться до полного останова,
т.е., до угла раскрыва
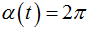 .
.
Под углом раскрыва
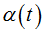 , в данном случае, будем понимать угол, отсчитываемый от
оси
O′X′ до замыкающего элемента системы
тел.
, в данном случае, будем понимать угол, отсчитываемый от
оси
O′X′ до замыкающего элемента системы
тел.
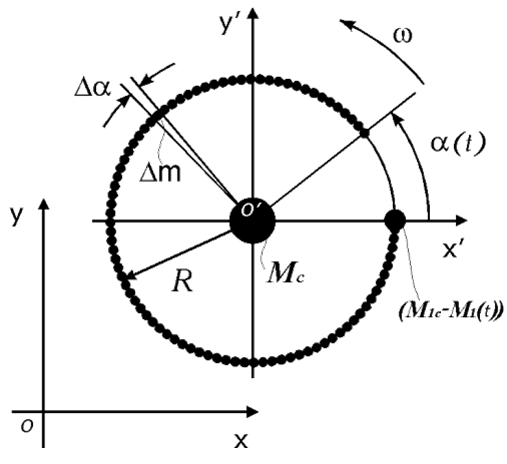
В начальный момент времени
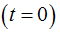 :
: 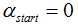 (для данной задачи).
(для данной задачи).
Угол раскрыва изменяется от 0 до 2π :
|
|
(1) |
Время, за которое угол раскрыва меняется от 0 до 2π , назовем рабочим периодом, или рабочим циклом T .
Будем считать, что вся
механическая система имеет две степени свободы (перемещение по
осям X и Y).
Примем условие, что существует ограничение поворота всей
системы.
(Примечание. Наложенное ограничение вполне допустимо,
поскольку может быть реализовано в условиях замкнутой системы.
См. раздел
2.5)
Построим две системы координат: неподвижную XOY (абсолютная система координат) и подвижную X′O′Y′, связанную с центром масс Mc и с центром траектории подвижных элементов.
Никакая часть сайта не может быть воспроизведена в какой бы то ни было форме и какими бы то ни было средствами без письменного разрешения владельца авторских прав.
Заявка на изобретение №2006134543
// //
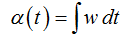 при
при 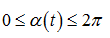
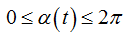 ,
при
,
при