|
Используя метод аналогий, можно
предположить, что должна существовать замкнутая механическая
система,
способная изменять свое положение в пространстве только с помощью внутренних
сил, без воздействия извне.
Метод аналогий.
Метод исследования какого-либо процесса, путём
замены его процессом,
описываемым таким же дифференциальным уравнением,
как и изучаемый процесс.
(Толковый словарь физических терминов)
Аналогия
между вращательным и поступательным движениями
« Я ценю умение строить аналогии, которые,
если они смелы и разумны,
выводят нас за пределы того, что пожелала нам открыть природа,
позволяя предвидеть факты ещё до того, как мы их увидим.
».
Ж.Л.Д’Аламбер
Между движением твердого тела вокруг неподвижной
оси и движением отдельной материальной точки (или поступательным движением
тела) существует тесная и далеко идущая аналогия. Каждой линейной величине
из кинематики точки соответствует подобная величина из кинематики вращения
твердого тела. Координате s соответствует
угол φ , линейной
скорости v - угловая скорость
w , линейному (касательному)
ускорению а - угловое ускорение
ε .
Сравнительные параметры движения:
|
Поступательное
движение
|
Вращательное
движение
|
|
Перемещение
|
S
|
Угловое перемещение
|
φ
|
|
Линейная скорость
|
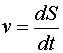 |
Угловая скорость
|
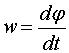 |
|
Ускорение
|
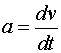 |
Угловое ускорение
|
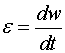 |
|
Масса
|
m
|
Момент инерции
|
I
|
|
Импульс
|
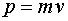 |
Момент импульса
|
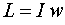 |
|
Сила
|
F
|
Момент силы
|
M
|
Таблицу можно продолжать и далее.
Работа:
Кинетическая энергия
Выражения для вращательного движения напоминают соответствующие
выражения поступательного движения.
Они получаются из последних формальной заменой
m → I , v → w , p → L
Выражения имеют не просто формальное сходство.
Поступательное движение можно рассматривать, как вращательное, с
радиусом вращения, стремящимся к бесконечности, и угловой скоростью,
стремящейся к нулю.
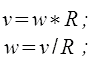
Представленная таблица не может претендовать на всю полноту охвата
аналогичных значений.
Для вращательного и поступательного движений формулируются и аналогичные
законы:
|
Закон сохранения
импульса (ЗСИ )
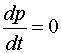 ,при Fвнеш
= 0
,при Fвнеш
= 0
|
Закон сохранения
момента импульса (ЗСМИ )
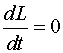 ,
при Mвнеш
= 0 ,
при Mвнеш
= 0
|
Эти законы формулируются следующим образом:
|
«Если геометрическая сумма внешних сил, действующих на систему,
равна нулю, то импульс системы сохраняется, т.е. не меняется
со временем. В частности, это имеет место, когда система
замкнута»
|
«Если момент внешних сил относительно неподвижного начала
О равен нулю, то момент импульса системы относительно
того же начала остается постоянным во времени»
|
|
[Д.В.Сивухин. Общий Курс
Физики. т.I Механика]
|
В классической механике закон сохранения импульса обычно выводится как
следствие законов Ньютона. Однако, этот закон сохранения верен и в случаях,
когда Ньютоновская механика неприменима (релятивистская физика, квантовая
механика). Он может быть получен как следствие интуитивно-верного утверждения
о том, что свойства нашего мира не изменятся, если все его объекты (или
начало отсчета!) переместить на некоторый вектор r.
В настоящее время не существует каких-либо экспериментальных фактов,
свидетельствующих о невыполнении закона сохранения импульса.
Закон сохранения момента импульса является следствием утверждения о
том, что свойства окружающего мира не изменяются при поворотах (или
повороте системы отсчета) в пространстве. Момент импульса системы
точечных тел L определяется как сумма моментов каждой из точек
и сохраняется во времени при условии равенства нулю момента внешних
сил. Данные законы относятся к глобальным законам сохранения.
Ответ на естественный вопрос о том, почему справедливы законы сохранения,
в физике был найден сравнительно недавно. Оказалось, что законы
сохранения возникают в системах при наличии у них определенных элементов
симметрии. (Элементом симметрии системы называется любое преобразование,
переводящие систему в себя, т.е. не изменяющее ее).
Немецкий математик Эмми Нётер в 1918 году математически доказала связь между
законами сохранения и симметрией, которой обладают в физике законы природы.
В упрощенной формулировке теорема Нётер гласит, что если свойства системы
не меняются от какого-либо преобразования переменных, то этому соответствует
некоторый закон сохранения.
Теорема Нётер - самое простое и универсальное средство, позволяющее
находить законы сохранения в классической механике, квантовой механике,
теории поля и т.д.
Вот как выглядят доказательства ЗСИ и ЗСМИ на основании свойства симметрии
пространства
[Д.В.Сивухин. Общий Курс Физики. т.I Механика.(гл.Y,§38)]:
.........
…4.Перейдем к доказательству закона сохранения
импульса. Допустим, что механическая система замкнута. Все силы F1
, F2 , ..., действующие на материальные точки системы, являются
силами внутренними, внешних сил нет. Перенесем систему из произвольного
положения 1 в другое произвольное положение 2, чтобы все материальные
точки ее претерпели одно и то же смещение r, и притом так, чтобы
их скорости остались прежними по величине и направлению. Ввиду однородности
пространства, на такое перемещение
не требуется затраты работы. Но эта
работа представляется скалярным произведением (F1 +F2
+ ...)r . Значит,
оно равно нулю, каково бы ни было смещение r. Отсюда
следует, что для замкнутой системы F1 +F2 + ...=0.
А это есть как раз то условие, при выполнении которого из второго закона
Ньютона получается закон сохранения импульса.
5. Закон сохранения момента импульса
для замкнутой системы доказывается в точности так же. Используя изотропию
пространства, можно доказать, что геометрическая сумма моментов внутренних
сил, действующих в системе, равна нулю: М1 +М2
+...=0. Отсюда немедленно следует рассматриваемый закон
..........
Как видно, доказательства очень похожи.
При всей схожести поступательного и вращательного движений, у них есть
и различия.
Одно из них и рассматривается в данной статье.
Существует явление, вступающее, казалось бы, в противоречие с ЗСМИ.
Замкнутую механическую
систему можно повернуть на любой угол
с помощью одних только внутренних сил.
|
И не только повернуть, но и заставить
вращаться.
Как можно повернуть механическую систему с помощью одних только внутренних
сил?
Рассмотрим пример.
Допустим, у нас имеется два уравновешенных тела, закрепленных соосно.
Тела имеют возможность вращаться относительно друг друга. Одно из тел
(зеленый контур, красный радиус) способно изменять свои геометрические
размеры, изменяя, тем самым, свой момент инерции (Iv).
Допустим, максимальное значение Iv max этого тела
соответствует значению Ic второго тела (синий контур,
пурпурный радиус). Минимальное значение Iv min значительно
меньше Iv max.
Рассмотрим циклы движения
данной механической системы.
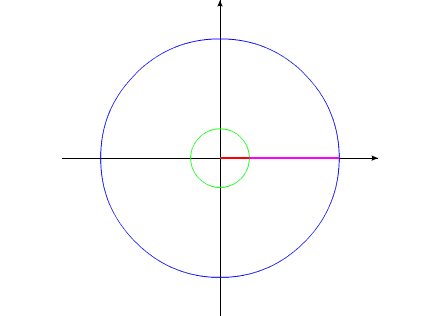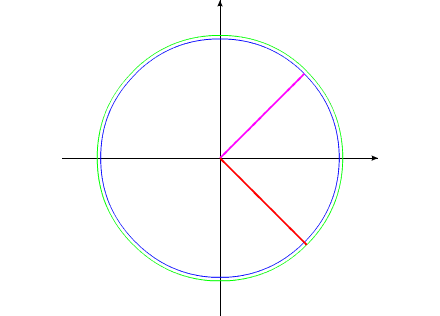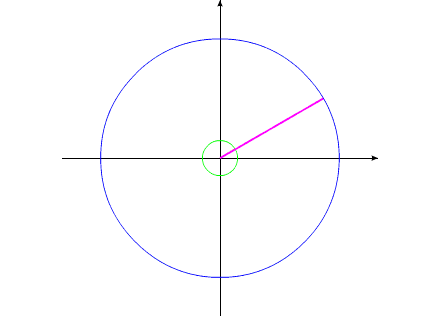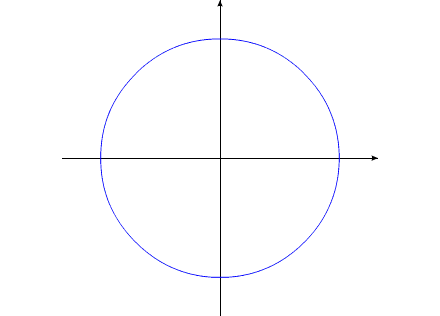
Рис.1
Тело с переменным Iv приобретает максимальные геометрические
размеры. (За счет внутренней энергии, разумеется).
За счет той же внутренней энергии создадим
внутренний момент, действующий одинаково на оба тела. Под действием
этого момента, тела начинают поворачиваться в противоположные направления.
Можно остановить движение обоих тел в
любой момент времени. Поскольку моменты инерции обоих тел равны, то
и угловые положения оба тела займут одинаковые (по абсолютной величине).
В момент останова, угловое положение всей системы осталось прежним.
Не изменится это угловое положение и тогда, когда мы начнем изменять
геометрические размеры одного из тел.
Уменьшив геометрический размер, и соответственно
момент инерции одного из тел, попробуем свести оба тела к прежним угловым
положениям этих тел, с помощью силового момента, направленного в другую
сторону.
Вот тут и происходит интересное.
Поскольку моменты инерции обоих тел уже
различны, то оба тела повернутся на разные углы. Можно опять увеличить
размеры одного из тел. Система вновь будет такой, как и прежде.
Почти…
На самом деле, вся система оказывается повернутой на некоторый угол.
Величина этого угла пропорциональна разнице моментов инерции
двух тел.
Эти циклы движения можно повторять.
И оказывается, что система вращается!
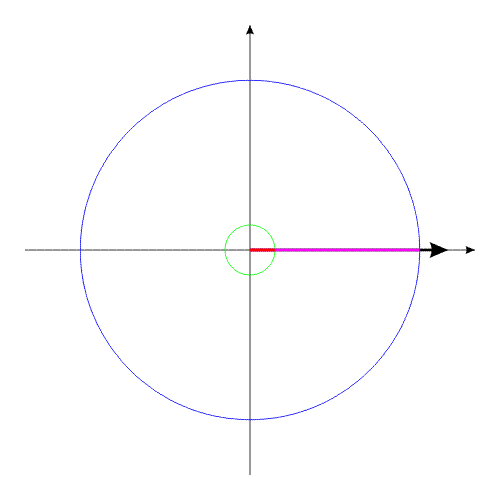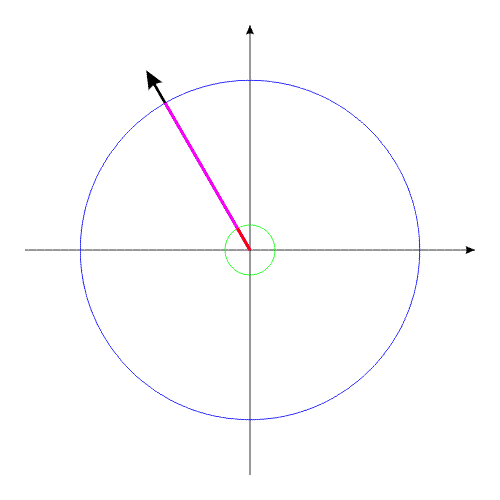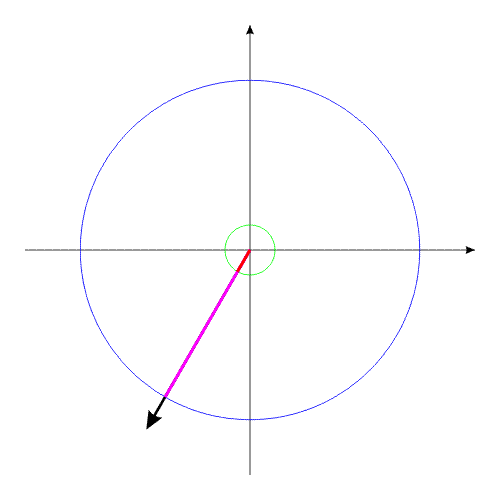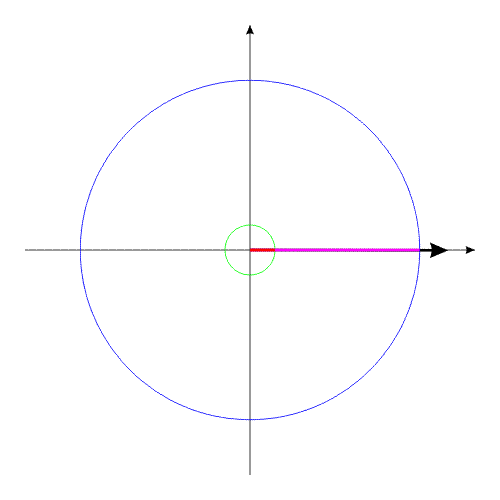
Рис.2
Причем, вращается совсем неплохо!
Допустим, компоненты системы изменяют свои геометрические размеры таким
образом, что суммарный момент инерции всей системы остается без изменений.
Изображенную на рис.3 систему можно рассматривать,
как взаимодействие тел с переменным моментом инерции, при неизменной
массе и неизменном моменте инерции всей системы в целом.
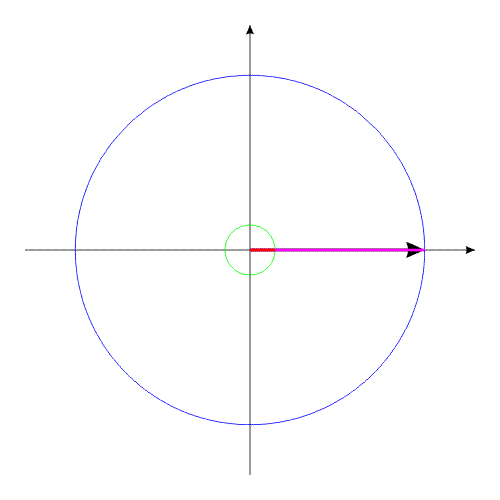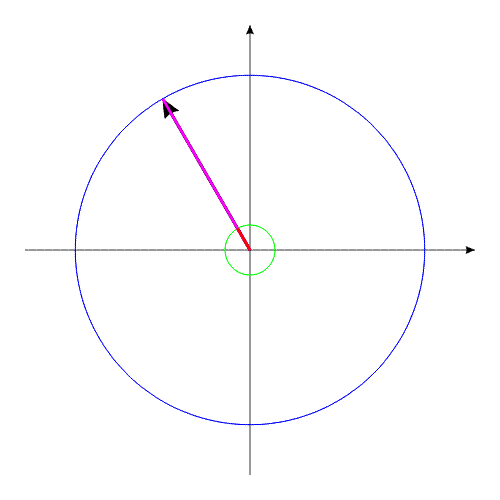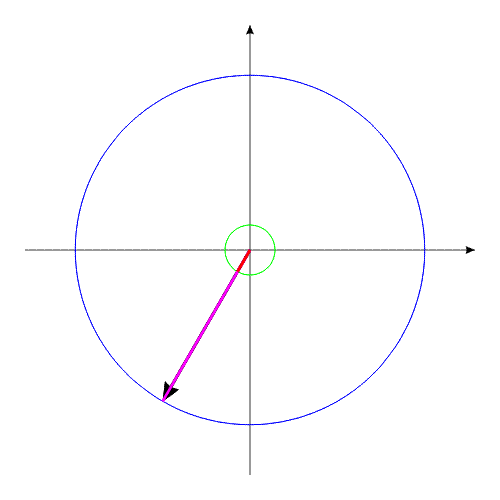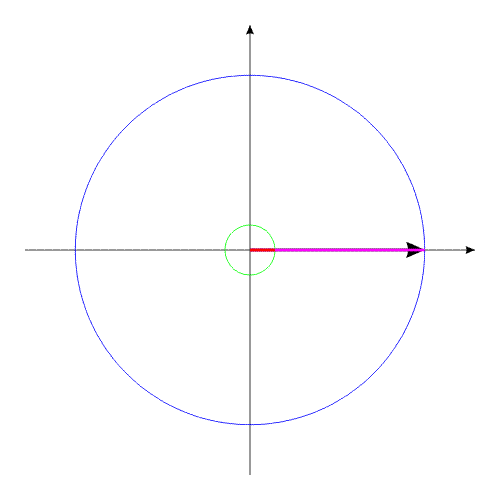
Рис.3
Система, изображенная в анимационном
рис.3, совершает полный оборот за 16 секунд.
Можно даже вычислить скорость вращения этой системы:
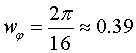 [рад/с]
[рад/с]
Но, на самом деле, нельзя говорить об этой величине,
как о «скорости вращения системы». Правильнее будет звучать:
«скорость процесса изменения углового положения», так
как величина wφ
не является мерой кинетического состояния данной системы, поскольку
кинетическая энергия системы не изменяется.
Рассмотренное движение является безынерционным
(движением без инерции!). Если остановить относительные
перемещения компонентов внутри замкнутой системы, движение
wφ немедленно
прекращается. К величине wφ
более всего подходит название скорость
прецессии.
безинерционное
В процессе подобного вращения не нарушается ЗСМИ, поскольку
суммарный момент импульса всех компонентов системы, в каждый момент
времени, равен нулю.
В то же время можно определить момент силы, эквивалентный внешнему моменту
силы, который необходимо было бы приложить к системе, чтобы вызвать
подобное перемещение.
Именно – эквивалентный, поскольку для рассматриваемой ситуации,
внешний силовой момент равен нулю.
Выводы, которые можно сделать на основании приведенного примера:
- в рамках Закона Сохранения Момента Импульса можно изменять
угловые координаты замкнутой механической системы только за счет
внутренних сил;
- важную роль при организации углового перемещения с помощью
внутренних сил, играет изменение момента инерции компонентов системы;
- угловое перемещение всей системы - безынерционно;
- скорость изменения угловых координат, имея размерность такую
же, как и угловая скорость, скоростью может считаться только формально.
Вернемся к доказательствам ЗСИ и ЗСМИ на основании
свойства симметрии пространства.
Доказательства строятся на допущении некоторого смещения системы (поворота,
в случае ЗСМИ).
Но в случае вращающейся системы, это смещение действительно можно произвести
за счет внутренней энергии.
То есть, смещение не виртуально, а вполне реально.
В большой таблице аналогичных выражений для вращательного и поступательного
перемещений, появляется большая пустая ячейка:
|
Перемещение
за счет внутренних сил
?
|
Поворот за счет внутренних сил
φ≠const
при:
∑Li=0,
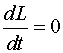 ,
Mвнеш
= 0 ,
Mвнеш
= 0
|
Перемещение за счет внутренних сил?
В случае с поступательным перемещением, такое, кажется, недопустимо.
На этот счет даже существует «Теорема о движении центра масс», которая,
на первый взгляд, не допускает подобное перемещение:
«Центр масс системы движется как материальная точка, масса которой
равна суммарной массе всей системы, а действующая сила — геометрической
сумме всех внешних сил, действующих на систему».
Значит, пустую ячейку в таблице должна занимать данная теорема?
Но метод аналогий позволяет предположить, что и для линейно перемещающейся
системы, должны существовать возможности, присущие вращающейся системе.
Это предположение строится на аналогичности уравнений движения вращательного
и поступательного движений.
Ячейка должна быть заполнена, примерно, следующим содержанием:
|
Перемещение
за счет внутренних сил
s≠const
при:
∑ pi=0,
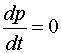 ,
Fвнеш
= 0 ,
Fвнеш
= 0
|
Это выражение получается в результате формальной замены
φ → S
, M → F , L → p
Выводы, которые можно сделать с помощью
метода аналогий:
- возможно существование механической системы, которая способна
линейно перемещаться только за счет внутренних сил;
- линейное перемещение может осуществляться за счет изменения
параметра, аналогичного моменту инерции, а именно – массы;
- линейное перемещение всей системы должно быть безынерционным;
-
«скорость» перемещения подобной системы не
будет являться мерой кинетического состояния, т.е. в процессе перемещения
суммарный импульс компонентов системы будет оставаться неизменным.
Поскольку «скорость» при таком движении является величиной формальной,
её появление не может служить признаком нарушения «Теоремы о движении
центра масс».
Варипенд
(Varipend)
Свойства механической системы, под названием "варипенд",
полностью удовлетворяют перечисленным предположениям.
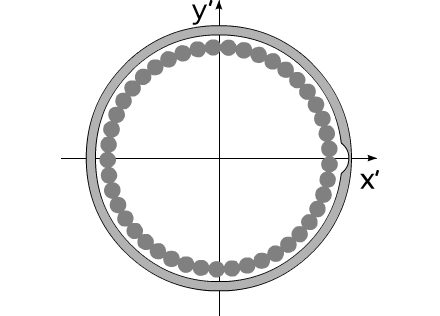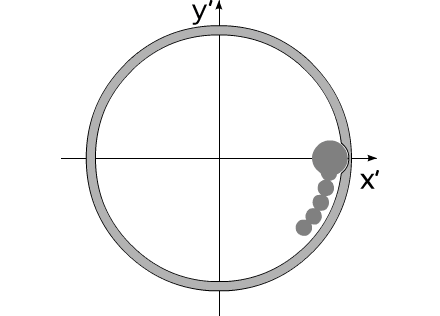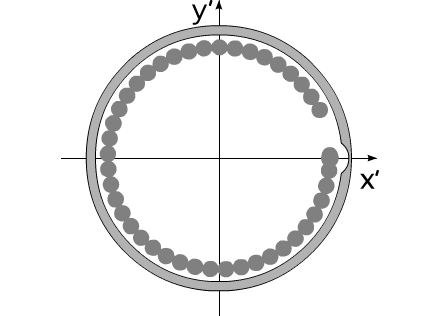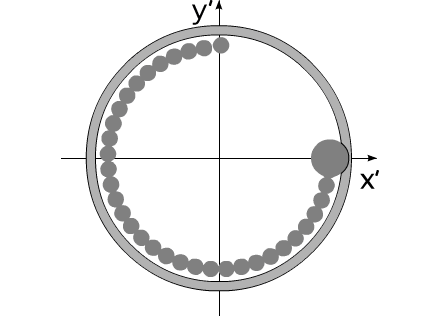
Рис.4
Название "варипенд" получено от слияния двух слов:
varipend =variable +pendulum (переменный маятник).
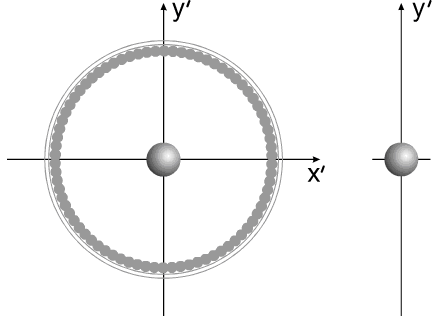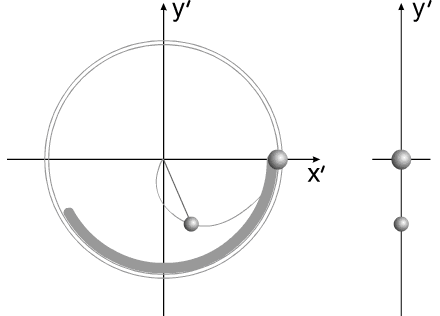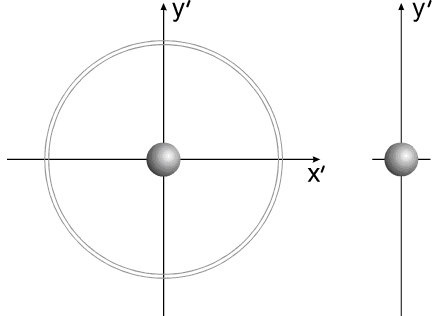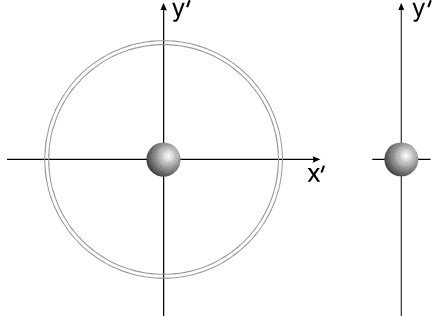
В процессе перемещения рабочей массы и её остановке
в "корпусе" системы, движение центра масс рабочего вещества можно рассматривать,
как движение маятника переменной длины и переменной массы. (В
системе координат, связанной с корпусом)

Рис.5
Или, в проекции на одну координату:
(Такой случай перемещения центра масс возможен при перемещении
двух рабочих масс, вращающихся в противоположных направлениях.)
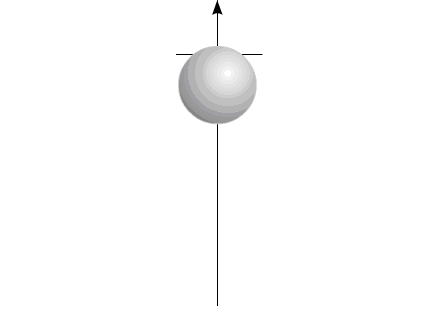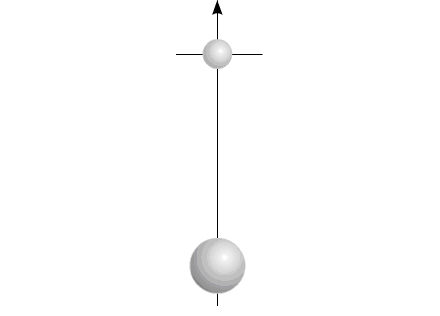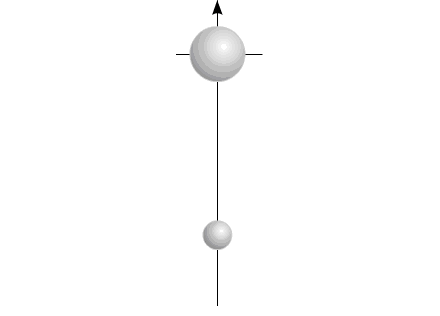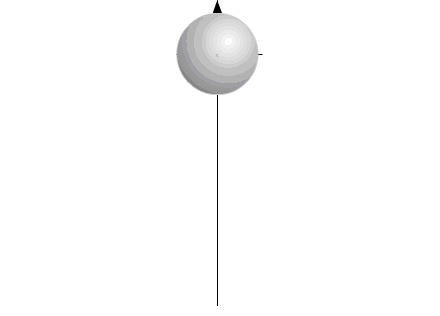
Рис.6
Изменяющийся размер компонентов на рисунке символизирует
изменение массы элементов системы:
рабочего вещества, уменьшающего свою массу за рабочий
период,
и корпуса системы, увеличивающего свою массу за счет
присоединения частиц рабочего вещества.
| При неизменной общей
массе, всю систему можно рассматривать, как взаимодействие компонентов
переменной массы. |
Единственной причиной
изменения импульса
корпуса является приобретение корпусом элементарных импульсов рабочей
массы. При этом корпус увеличивает свою массу.
Единственная причина
изменения импульса
рабочей массы – потеря элементарных импульсов частиц рабочей массы.
При этом масса рабочего вещества уменьшается.
При этом
изменение импульса
всей системы равно нулю.
И суммарный импульс
всей системы также равен нулю!
В
одном из расчетов перемещения "варипенда" используется уравнение
движения тела переменной массы – уравнение Мещерского.
Расчет перемещения данной механической системы с помощью
уравнений Лагранжа также приводит к
интересному результату...
На рис.4 представлена постановка задачи "варипенд".
Решение этой задачи выглядит следующим образом:
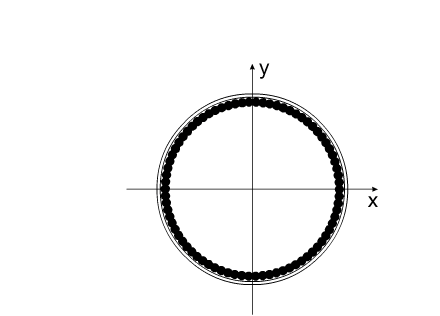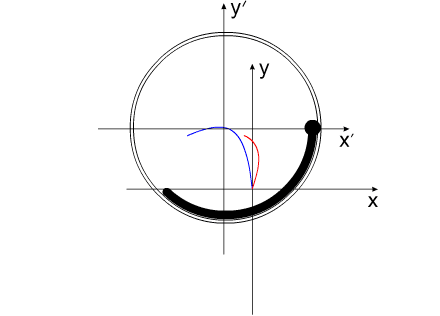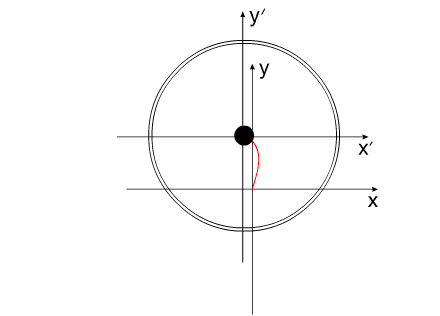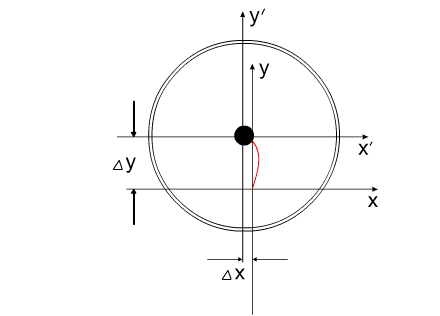
Синим цветом показана траектория перемещения
корпуса.
Красным - перемещение Центра Масс всей системы.
рис.7
При перемещении "варипенда"
не совершается работа.
Если рассматривать "варипенд" в абсолютной системе координат, то при
повторении внутренних циклов перемещения рабочего вещества, "варипенд"
непрерывно изменяет свое положение в пространстве:
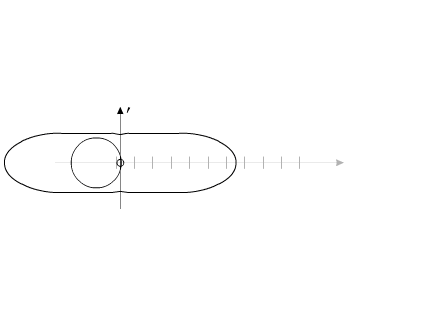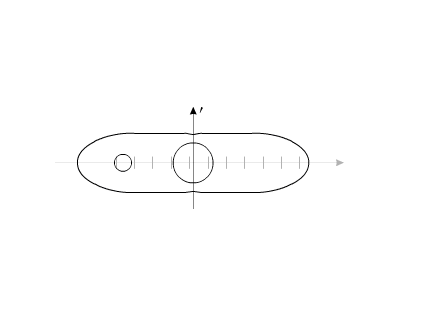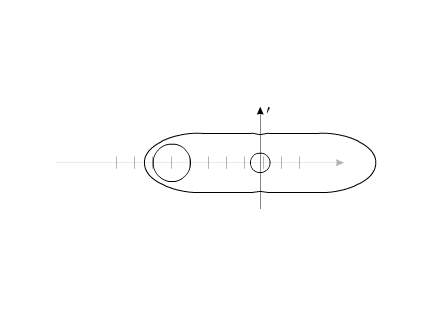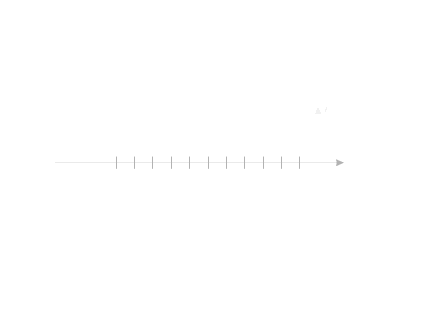
Рис.8
Можно провести аналогию с рисунком 3.
Система, изображенная на рис.8, перемещается на расстояние 55 мм за
20 секунд.
Казалось бы, можно подсчитать скорость "варипенда":
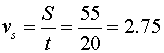 [мм/с]
[мм/с]
Но так как в процессе перемещения суммарный импульс системы остается
неизменным, величина vs
будет являться величиной формальной, определяющей только изменения
координат центра масс. Эта величина никак не связана с импульсом
всей системы.
Перемещение "варипенда" является
безынерционным.
Если остановить относительное перемещение рабочей
массы внутри замкнутой механической системы, вся система мгновенно прекратит
свое движение.
Математические расчеты, описывающие свойства механической системы под
названием «варипенд», можно посмотреть по адресу:
https://varipend.narod.ru
Примечание
Во многих учебных изданиях по Теоретической Механике,
приводятся примеры поворота замкнутой механической системы за счет внутренних
сил.
Например, человек способен повернуть себя на скамье Жуковского, совершая
некоторые вращения руками.
Поворачивая массивные тела в космическом летательном аппарате, производят
угловую ориентацию этих аппаратов.
Космонавт, находясь в невесомости, также может повернуть свой корпус,
совершив несколько оборотов рукой.
Однако, на самом деле, во всех приведенных примерах поворот системы
отсутствует.
Приведенные примеры демонстрируют, если можно так выразиться, "теорему
о сохранении углового положения" замкнутой механической системы.
Попытаюсь пояснить свои слова.
Если моменты инерции компонентов системы не изменяются и внешний момент
отсутствует, то можно записать:
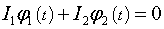
Это легко проверить.
Допустим, мы поворачиваем два тела друг относительно друга.
Если после остановки поворачивать компоненты в противоположную сторону,
система обязательно займет точно такое же угловое положение, которое
было в начальный момент времени.
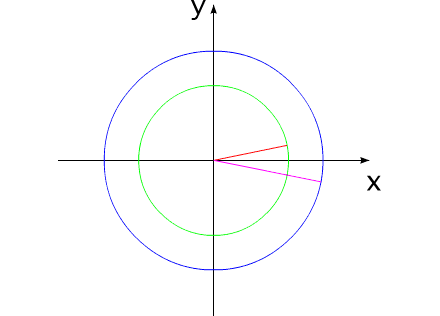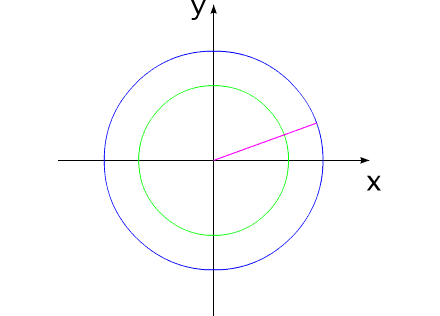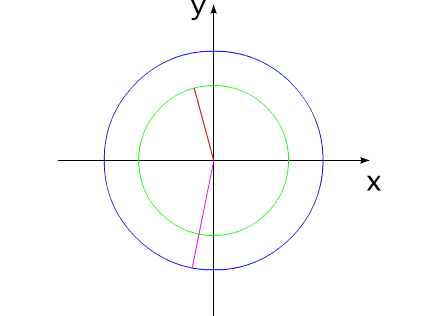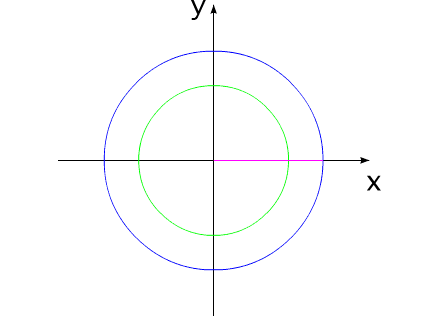
Рис.9
На рис.9 два тела сначала поворачиваются на некоторый
угол, а затем поворачиваются в противоположную сторону на точно такие
же углы. При этом система занимает свое прежнее угловое положение.
Иллюзия поворота всей системы возникает из-за того, что угловая
функция периодична. Как только угловые положения компонентов превышают
угол 2π,
возникает ощущение, что система повернулась. Но это не так. Конечно
же, углы необходимо продолжать отсчитывать и при превышении угла 2π.
Аналогичным примером линейного перемещения может служить случай
взаимодействия двух тел, обладающих неизменной массой:
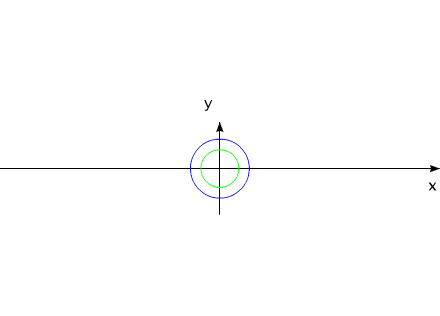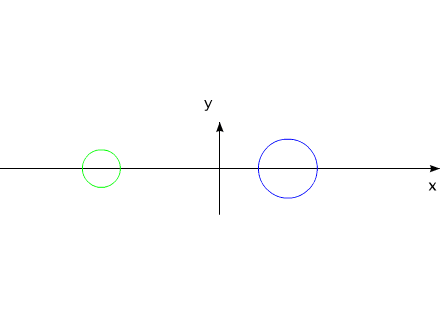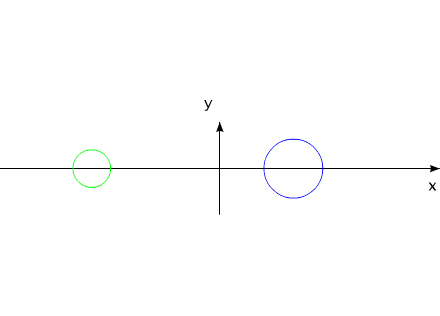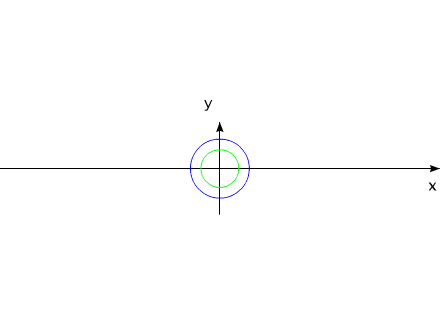
Рис.10
Тела могут удалятся друг от друга, за счет внутренних сил, приближаться,
но для данной системы всегда будет выполняться соотношение:
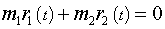
Это - следствие теоремы о движении центра масс....
А как будут выглядеть те же выражения для условий
системы, состоящей из компонентов с переменным моментом инерции
(переменной массой)?:
С.Бутов
7 июля 2007
"
... аналогия является специфическим случаем симметрии, особым видом
единства сохранения и изменения. Следовательно, использовать в анализе
метод аналогии, — значит действовать в соответствии с принципом симметрии.
Аналогия не только допустима, но и необходима в познании природы вещей...."
[Овчинников Н. Ф. Принципы сохранения,.М.,1966]
Новиков Н.Б.
"1000 аналогий,
изменивших науку".


© ButovSV
07/07/2007
Защищено
законодательством Российской Федерации по авторским правам.
Никакая часть сайта не может быть воспроизведена в какой бы то ни
было форме
и какими бы то ни было средствами без письменного разрешения владельца авторских
прав.
|
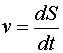
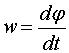
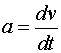
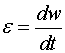
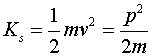
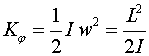
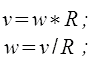
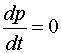 ,при Fвнеш
= 0
,при Fвнеш
= 0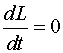 ,
при Mвнеш
= 0
,
при Mвнеш
= 0


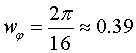 [рад/с]
[рад/с]





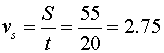 [мм/с]
[мм/с]
