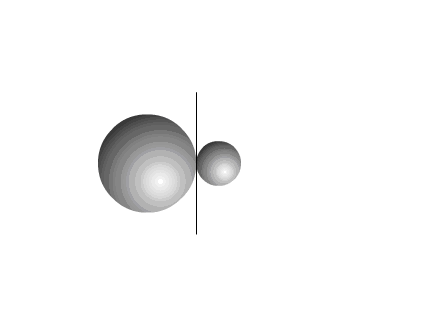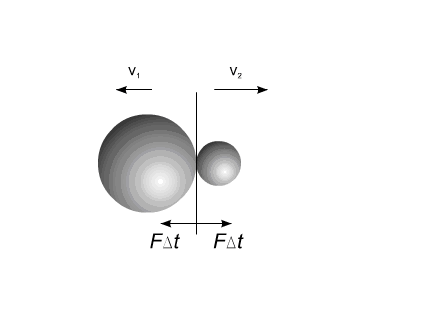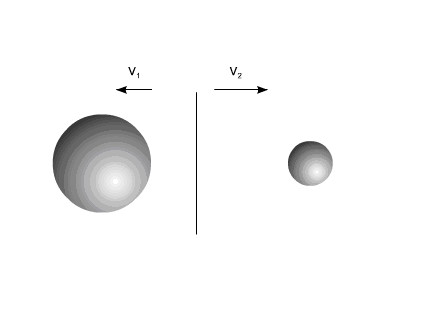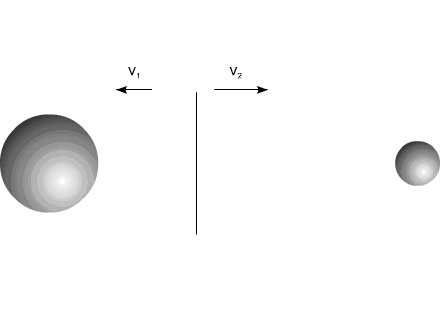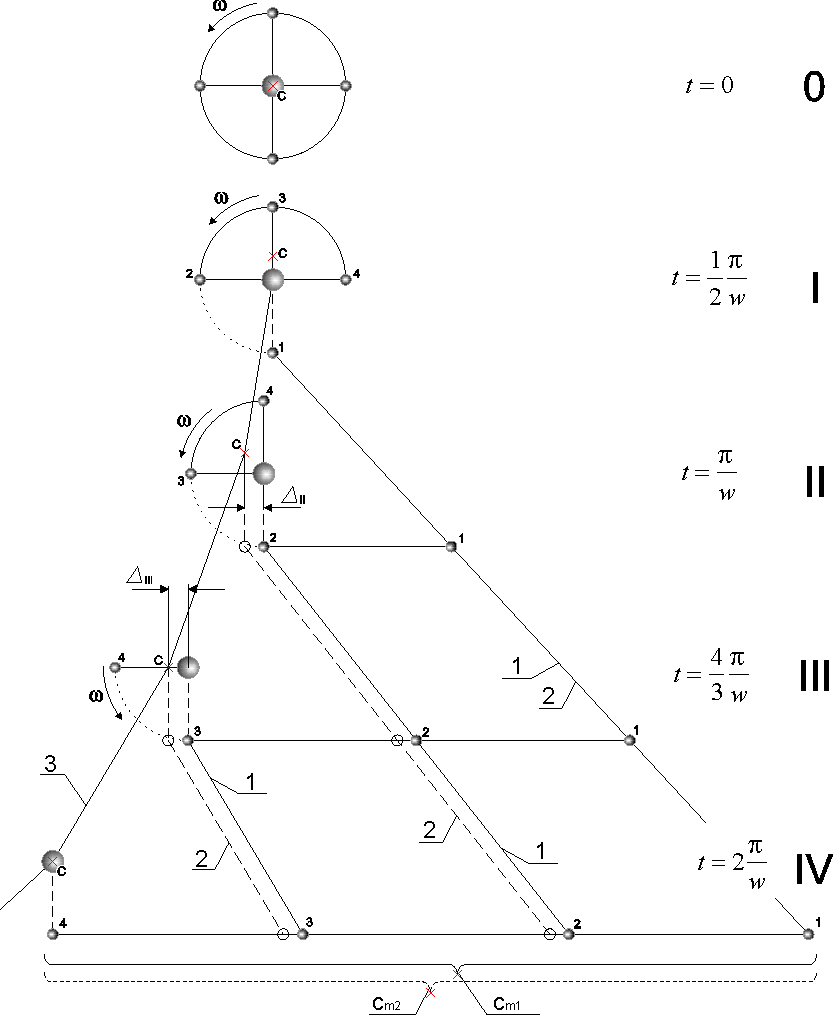Нереактивное перемещение.
Нереактивное перемещение.

Автор статьи не придумывает
новые физические законы, и ни в коем случае не пытается нарушить действующие.
Для замкнутой системы, то есть системы, не испытывающей
внешних воздействий, или в случае, когда геометрическая сумма действующих
на систему внешних сил равна нулю, имеет место закон сохранения количества
движения. При этом количество движения отдельных частей системы (например,
под действием внутренних сил) могут изменяться, но так, что величина
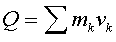 остаётся постоянной.
остаётся постоянной.
Этот закон объясняет такие явления, как реактивное
движение, отдачу (или откат) при выстреле, работу гребного винта или
вёсел и др.
Например, если рассматривать ружье и пулю как одну
систему, то давление пороховых газов при выстреле будет для этой системы
силой внутренней и не может изменить количество движения системы, равное
до выстрела нулю. Поэтому, сообщая пуле количество движения
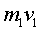 , направленное к дульному срезу, пороховые газы сообщат
одновременно ружью численно такое же, но противоположно направленное
количество движения
, направленное к дульному срезу, пороховые газы сообщат
одновременно ружью численно такое же, но противоположно направленное
количество движения
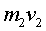 , что вызовет отдачу. Из равенства
, что вызовет отдачу. Из равенства
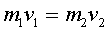 (где
(где
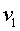 ,
,
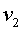 — численные значения скоростей) можно, зная скорость
— численные значения скоростей) можно, зная скорость
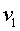 пули при вылете из ствола, найти наибольшую скорость
пули при вылете из ствола, найти наибольшую скорость
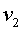 отдачи (а для орудия — отката).
отдачи (а для орудия — отката).
В приведенном примере тела приобретают скорости под
действием импульса силы
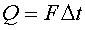 , величина которого равна для обоих тел, но противоположна
по направлению (Рис.1).
, величина которого равна для обоих тел, но противоположна
по направлению (Рис.1).
После воздействия импульса силы тела двигаются прямолинейно
и равномерно.
Центр масс всей системы, после разлета компонентов, сохраняет свою первоначальную
скорость.
Если рассматривать ракету и продукты сгорания ракетного
топлива как единую механическую систему, то центр масс этой системы
также сохраняет неизменным свое положение. (В системе отсчета, связанной
с точкой старта.)
В то же время возможна ситуация, когда компоненты системы
тел приобретают количество движения не за счет явно выраженного импульса
силы.
Компоненты системы тел могут приобрести количество движения, потому
что уже обладают импульсами, имеют какую-то кинетическую энергию.
Рассмотрим следующий пример.
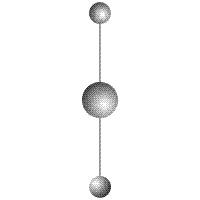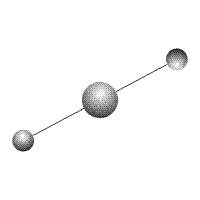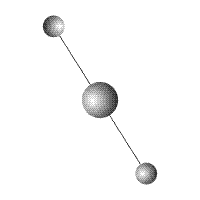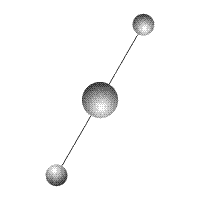
Рис. 2
Вокруг тела массой
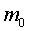 вращаются два тела одинаковой массы
вращаются два тела одинаковой массы
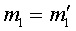 (Рис.2). Все тела соединены
жесткими неразрывными связями. Вращение с угловой скоростью
(Рис.2). Все тела соединены
жесткими неразрывными связями. Вращение с угловой скоростью
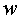 происходит вокруг общего центра масс системы, совпадающего,
в данном случае, с центром масс тела
происходит вокруг общего центра масс системы, совпадающего,
в данном случае, с центром масс тела
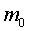 . Система тел уравновешена. Ее центр масс неподвижен. Проекции
количества движения на оси координат равны нулю.
. Система тел уравновешена. Ее центр масс неподвижен. Проекции
количества движения на оси координат равны нулю.
Если в некоторый момент времени разорвать одну из
связей, то компоненты системы начнут перемещаться в противоположных
направлениях.

Рис. 3
После обрыва связи система распадается на два компонента:
тело
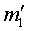 и систему из двух связанных тел
и систему из двух связанных тел
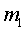 и
и
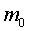 (Рис.3).
(Рис.3).
Тело
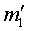 будет двигаться прямолинейно и равномерно по касательной
к траектории своего движения в момент обрыва связи.
будет двигаться прямолинейно и равномерно по касательной
к траектории своего движения в момент обрыва связи.
Система тел
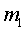 и
и
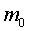 также будет двигаться прямолинейно и равномерно. Количество
движения этой системы, по абсолютной величине, будет равно количеству
движения
также будет двигаться прямолинейно и равномерно. Количество
движения этой системы, по абсолютной величине, будет равно количеству
движения
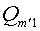 :
:
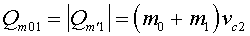
, где
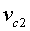 — скорость центра масс системы тел
— скорость центра масс системы тел
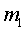 и
и
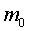 .
.
Следует подчеркнуть, что выражение «прямолинейно
и равномерно» относится только к центру масс рассматриваемой системы
(отмечен красным цветом на Рис.3).
Компоненты системы, в то же время, приобретают неравномерные относительные
скорости перемещения относительно общего центра масс.
Если тело
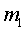 в начальный момент времени, сразу после обрыва связи,
двигается так же, как и тело
в начальный момент времени, сразу после обрыва связи,
двигается так же, как и тело
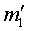 (по абсолютному значению), то для тела
(по абсолютному значению), то для тела
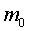 начальная скорость равна нулю.
начальная скорость равна нулю.
Таким образом, тело
 «запаздывает», его скорость заметно отстает от скорости
центра масс в начальный момент времени, сразу после обрыва связи. Можно
показать чуть помедленнее (рис.4).
«запаздывает», его скорость заметно отстает от скорости
центра масс в начальный момент времени, сразу после обрыва связи. Можно
показать чуть помедленнее (рис.4).
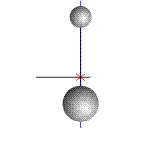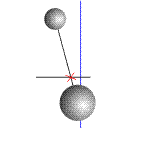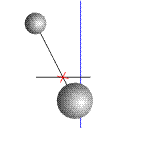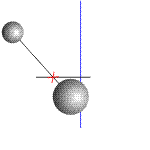
Рис. 4
Этот процесс «запаздывания» можно увеличить, "растянуть
во времени".
Допустим, на борту некоего летательного аппарата,
покоящегося в невесомости, установлена кольцевая центрифуга, равномерно
заполненная по всей окружности дробинками. Центрифуге придается вращательное
движение. Ось центрифуги совпадает с центром масс летательного аппарата.
В некоторый момент времени, дробинки начинают покидать центрифугу. Покидают
последовательно, друг за другом, из одной и той же точки, относительно
корпуса летательного аппарата.
Если бы дробинки отстреливались, как в примере с
ружьем и пулей, то после каждого отстрела дробинки, корпус летательного
аппарата приобретал бы импульс, равный по величине и противоположный
по направлению дроби.
В случае с центрифугой, «отстрела» нет.
Дробинка просто «отпускается», то есть разрывается связь, за счет которой дробинка осуществляла вращательное движение относительно оси центрифуги.
Отделившаяся от центрифуги дробинка не воздействует на корпус ракеты.
Не участвует непосредственно в процессе изменения импульса ракеты!
Корпус летательного аппарата изменяет свою скорость исключительно за счет импульса дробинок, оставшихся в центрифуге.
Для равномерно заполненной центрифуги, проекция суммарного импульса всех дробинок на ось движения равна нулю.
Если изъять одну дробинку из этой равномерной группы, то проекция суммарного импульса оставшихся дробинок будет равна импульсу одной изъятой дробинки. Только с другим знаком.
В процессе отделения дробинок, масса груза на центрифуге уменьшается.
При этом изменяется положение центра масс груза.
На Рис.5 представлен
графический вариант описанного процесса для случая с центрифугой, содержащей
4 груза-дробинки.
Предполагается, что поворот всей системы отсутствует. (Допустим, на
борту летательного аппарата установлены две одинаковые центрифуги, вращающиеся
в противоположные стороны.)
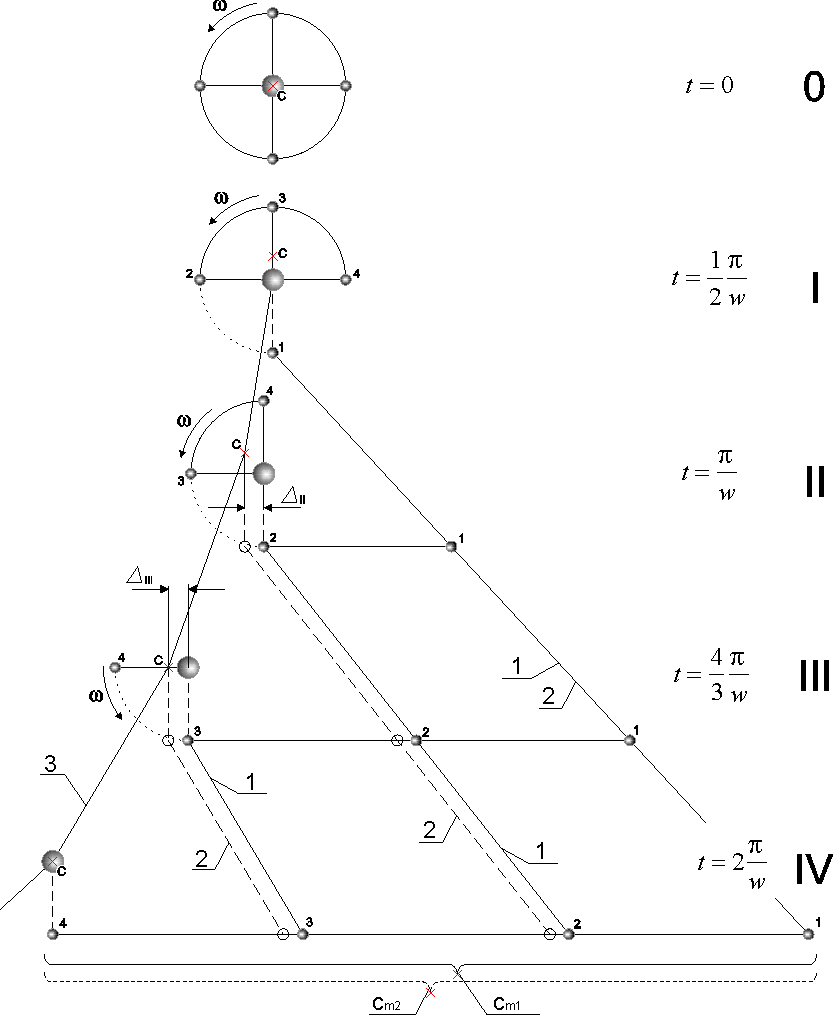
Рис. 5
В начальный момент 0 (Рис.5)
груз равномерно распределен. Центрифуга уравновешена и вращается с угловой
скоростью
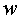 . Центр масс груза (точка «С») совпадает с осью
вращения центрифуги и центром масс корпуса летательного аппарата.
. Центр масс груза (точка «С») совпадает с осью
вращения центрифуги и центром масс корпуса летательного аппарата.
После каждого отделения дробинки (моменты I,II,III,IY
на рисунке), центр масс корпуса аппарата с разбалансированной
центрифугой движется прямолинейно и равномерно (ломаная линия 3).
Дробинки также движутся равномерно и прямолинейно
(прямые линии 1).
Но только первая и последняя дробинки (моменты I
и IY) отделяются из центра масс системы [корпус аппарата + центрифуга]
(в проекции на ось перемещения компонентов).
В моменты времени II и III грузы отделяются на некотором
расстоянии
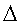 от центра масс системы [корпус аппарата + разбалансированная
центрифуга]. Происходит как бы «запаздывание» процесса отделения. "Запаздывание"
от равномерного и прямолинейного перемещения ЦМ.
от центра масс системы [корпус аппарата + разбалансированная
центрифуга]. Происходит как бы «запаздывание» процесса отделения. "Запаздывание"
от равномерного и прямолинейного перемещения ЦМ.
Для сравнения, на рисунке приведены возможные траектории
движения дробинок в случае их отстрела из центра масс системы
[корпус + центрифуга] (пунктирные линии 2 на рисунке). Под «отстрелом»,
в данном случае, подразумевается отделение частиц под воздействием импульса
силы, после которого частицы приобрели бы такую же относительную скорость,
как и при отделении от центрифуги. Каждый отстрел дробинки производился
бы из центра масс корпуса летательного аппарата с грузом оставшихся
дробинок. То есть из точки, которая отмечена на рисунке, как точка «С».
Эта точка двигается прямолинейно и равномерно после каждого «отстрела».
На рис.6 представлен
анимированный вариант рисунка 5.
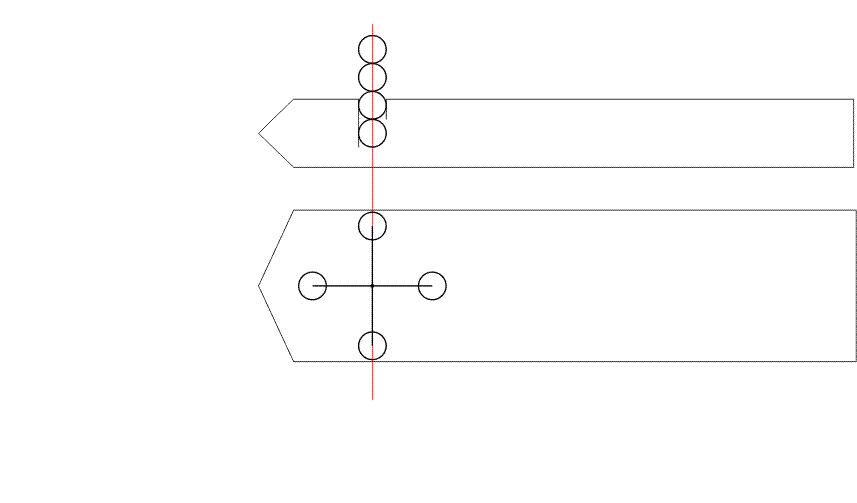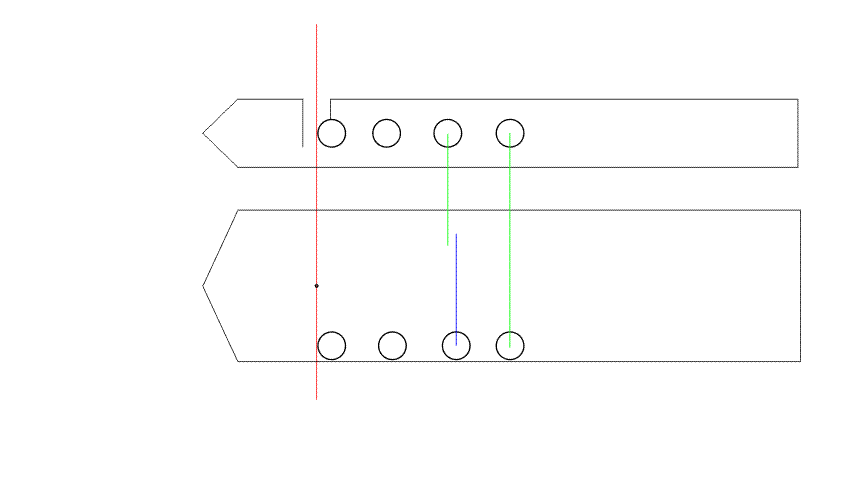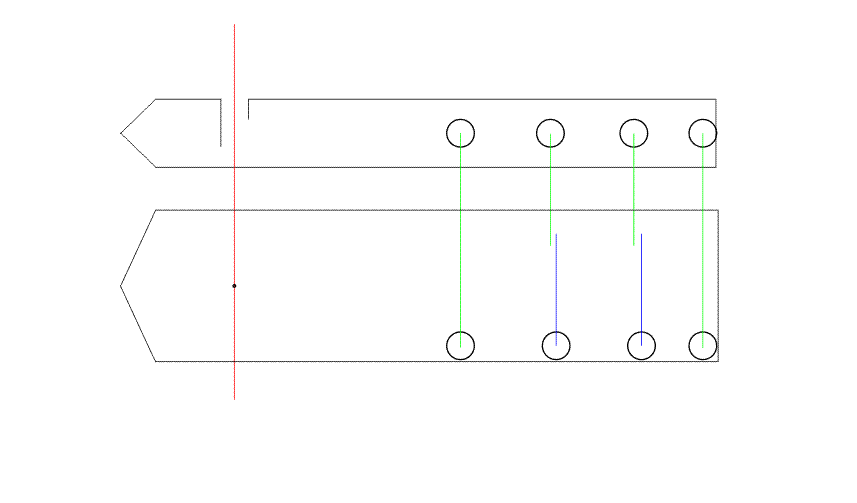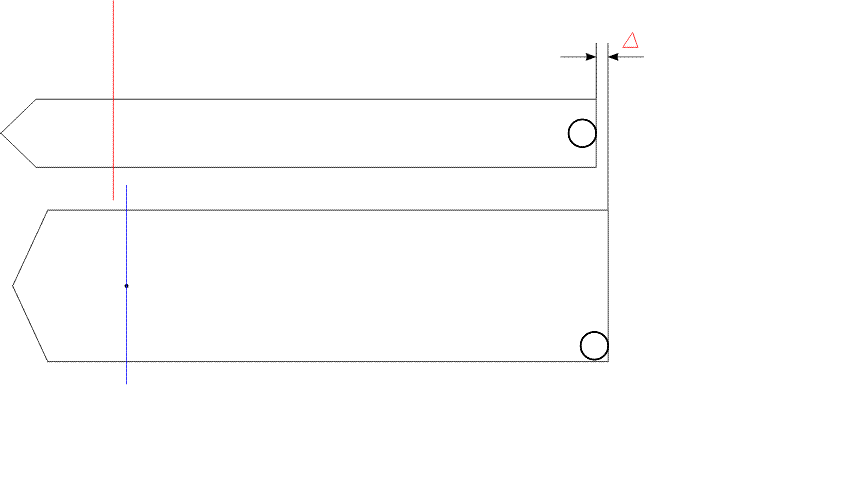
Рис. 6
После отделения, дробинки летят
до момента контакта с "задней стенкой" летательного аппарата.
Центр масс «цепочки» дробинок, отделившихся от центрифуги
(положение точки
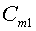 на Рис.5), смещен относительно
центра масс дробинок, которые были бы «отстрелены» (положение точки
на Рис.5), смещен относительно
центра масс дробинок, которые были бы «отстрелены» (положение точки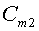 на Рис.5).
на Рис.5).
После соединения летящих дробинок с корпусом
летательного аппарата, скорость корпуса будет равняться начальной скорости
всей механической системы, или, в данном случае, нулю.
Но положение центра масс всей системы [корпус
+ груз] будем различным
для разных способов отделения частиц груза.
Итак:
Количество движения
дробинок как в случае "отстрела", так и в случае отделения
от центрифуги - одинаково.
На каждом этапе отделения
дробинок, импульс систем [корпус
+ "оставшийся груз"]
также имеет одинаковое значение.
А вот положение центров
масс двух механических систем в начальный и конечный моменты
времени - различны.
|
Графическое решение наглядно показывает, что центр масс механической
системы, при разных способах разделения компонентов, имеет различные
координаты. (Решение не только графическое.
Посмотреть графики перемещения
компонентов для условий конкретной задачи, можно здесь.)

Таким образом, предполагается, что существует возможность перемещения
замкнутой механической системы за счет внутренней энергии системы. При
таком перемещении не нарушается закон сохранения количества движения.
Смещение центра масс всей механической системы происходит в течение
всего периода отделения частиц груза от центрифуги.
Величина смещения пропорциональна радиусу центрифуги и массе груза
на центрифуге.
Можно допустить, что расстояние до "задней стенки летательного аппарата"
равно нулю, то есть частицы груза пролетают "нулевую" дистанцию.
Перемещение подобной механической системы изображено на
рис.7
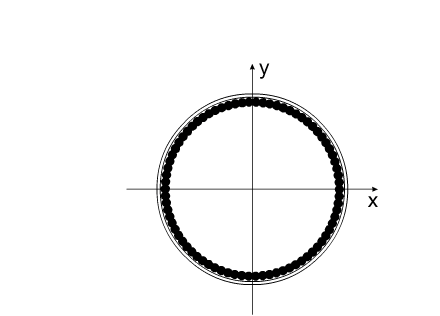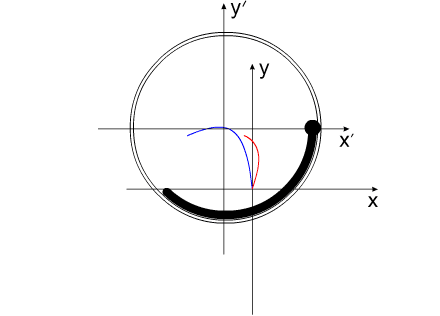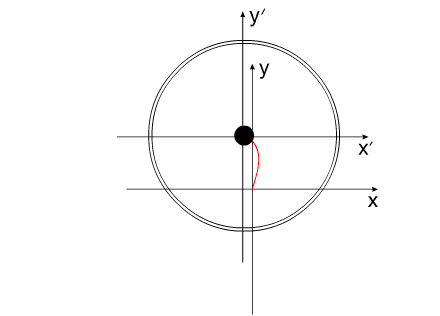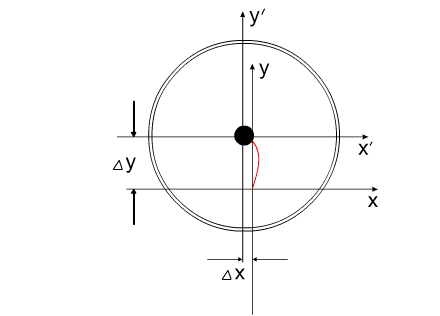
Синим цветом показана траектория перемещения корпуса.
Красным - перемещение Центра Масс всей системы
Рис. 7
.
Математические расчеты, описывающие данное явление, вы можете посмотреть по адресу:
https://varipend.narod.ru
С.Бутов
© ButovSV
12/04/2007
Защищено
законодательством Российской Федерации по авторским правам.
Никакая
часть сайта не может быть воспроизведена в какой бы то ни было форме
и какими бы то ни было средствами без письменного разрешения владельца
авторских прав


|