|
Содержание:
Rus
|
Можно организовать работу группы Силовых Элементов (СЭ) таким образом, что начало рабочего цикла у каждого СЭ будет отличаться от предыдущего СЭ. Допустим, фазовый сдвиг у каждого СЭ из группы n элементов будет равен
т.е., когда первый СЭ из группы начинает рабочий цикл, последний СЭ завершает его.
На Рис. 16 представлена условная схема работы группы СЭ из 8 элементов.
Рис. 17 Допустим, что каждый СЭ после завершения рабочего цикла сразу начинает новый рабочий цикл. Время восстановления СЭ в рабочее состояние опущено для упрощения. Масса подвижных элементов, участвующих в движении в системе из n СЭ:
При большом числе
n, т.е., соответственно, при малом
Среднее значение этой массы:
, где
На Рис. 18 представлен график изменения масс подвижных элементов системы из 4 СЭ.
Рис. 17 Центр масс каждого из СЭ перемещается по зависимости (8).
График перемещения центров масс подвижных элементов системы из 4 СЭ представлен на Рис. 18.
Рис. 18 Сумма количеств движений СЭ в системе координат, связанной с замкнутой механической системой, определяется выражением:
На Рис. 20 представлен график изменения количества движения системы СЭ с фазовым сдвигом.
Рис. 20
Среднее значение суммарного импульса СЭ в подвижной системе координат будет:
Из закона сохранения импульса замкнутой механической системы следует:
где: 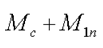 — масса части механической системы, с
центром масс которой связано начало отсчета подвижной системы
координат
X’O’Y’
.
— масса части механической системы, с
центром масс которой связано начало отсчета подвижной системы
координат
X’O’Y’
.
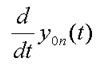 — скорость подвижной системы координат
X’O’Y’ в проекции на ось
Y неподвижной системы координат
XOY .
— скорость подвижной системы координат
X’O’Y’ в проекции на ось
Y неподвижной системы координат
XOY .
Часть выражения: 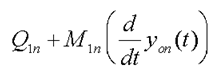 — определяет импульс СЭ в неподвижной
системе координат XOY .
— определяет импульс СЭ в неподвижной
системе координат XOY .
Решение дифференциального уравнения (45)
относительно
Анализ выражения
(46) показывает, что
система из
n СЭ, начало рабочего цикла каждого из которых
отличается от начала рабочего цикла предыдущего СЭ на величину
На Рис. 21
красным цветом изображена траектория движения системы из трех
СЭ.
Рис. 21 Расчет сделан из условия, что каждый СЭ после завершения рабочего цикла сразу начинает новый рабочий цикл. Время восстановления СЭ в рабочее состояние опущено для упрощения.
Система движется равномерно
только при
Скорость всей замкнутой системы есть производная по времени от координаты, определяющей центр масс системы:
Ускорение системы, как производная по времени от скорости, равно нулю:
То есть, в любой момент времени система перемещается без ускорения.
Можно рассчитать силу, с которой система СЭ способна перемещать всю механическую систему.
Сила, развиваемая одним СЭ определена выше (38). Для группы СЭ с фазовым сдвигом суммарная сила:
При большом количестве СЭ в группе, можно принять среднее значение суммарной силы:
По аналогии с гироскопами, у которых гироскопический момент есть результат кориолисовых сил инерции, можно сказать, что у СЭ сила перемещения есть результат центробежных сил инерции.
При непрерывной групповой работе каждый СЭ изменяет свою кинетическую энергию (39). За единицу времени, количество «потерянной» энергии равно количеству энергии, переданной СЭ для восстановления. При большом n и непрерывном восстановлении СЭ, можно считать работу по восстановлению СЭ равномерной. Мощность, необходимая для восстановления СЭ в рабочее состояние:
Примечание : Значение мощности
найдено из условия, что элементы подвижных систем СЭ полностью
останавливаются по завершении рабочего цикла. В реальных
устройствах это делать нецелесообразно. Рекомендуется изменять
скорость подвижных элементов только по одной координате.
|