| > | restart; |
Jet-not-Jet
Программа для расчета положения и скоростей объектов при реактивном и "нереактивном" разделении компонентов.
Экспорт из рабочего файла Maple, под условным названием
васькина_хнь22_vas_plus.mws
Дата создания: 01 апреля 2010г.
Нормальные расчеты можно посмотреть здесь
| > | with(plots): |
Объявление процедуры.
Параметр n - количество "дробинок"
Процедура для системы с центрифугой
| > | Non_jet:=proc(n) # |
Объявление глобальных переменных.
| > | global w,r,V,S,Vc,Sc,DD,DS,VDS,f,dt,Time,CMc,CM,MVc1,MVc2; |
w - угловая скорость вращения, const;
r - радиус, по которому движутся элементы системы;
V - таблица значений абсолютных скоростей отдельных дробинок после отделения;
S -таблица значений расстояний: от начала координат до положения дробинки по завершении всего цикла.
Vc -таблица значений скоростей ЦМ остатка.
Sc -таблица значений расстояний: от начала координат до ЦМ остатка.
DS -таблица значений расстояний: от ЦМ остатка до оси вращения, т.е до точки отделения частицы, так называемая величина "Delta";
DD -таблица значений "дельта дельты": отскок ЦМ остатка при отделении одной элементарной частицы;
VDS -таблица значений скоростей. Относительная скорость смещения оси вращения (т.е точки отделения частицы), относительно ЦМ остатка .;
f -таблица значений углов;
dt -интервал времени между отделениями частиц
Time -таблица значений времен. Совершенно простая и необязательная, но удобна при организации графика;
CMc -таблица значений положения ЦМ всей системы;
CM -таблица значений ЦМ "цепочки" отделившихся частиц в каждый момент времени;
MVc1 и MVc2 -таблицы значений импульсов "остатка" до отделения элементарной частицы и после.
Разница между этими значениями аналогична величине DD. Только это "скачок" импульса остатка, т.е. та величина, что и заставляет двигаться остаток.
dt -интервал времени между отделениями частиц.
Определяется, как деление всего времени (2Pi/w) на число элементарных частиц (n)
| > | dt:=2*Pi/(w*n); |
| > | m1:=M1c/n; |
Заполнение Time -таблицы значений времен. Совершенно простая и необязательная, но удобна при организации графика;
| > | for i from 0 to n do |
| > | Time[i]:=dt*i; |
| > | end do; |
Заполнение f -таблицы значений углов
| > | f[0]:=0; |
| > | df:=2*Pi/n; |
| > | for i from 1 to n do |
| > | f[i]:=i*df; |
| > | end do; |
| > |
Таблица суммарного импульса остатка до отделения
| > | MVc1[0]:=0; |
| > | for i from 1 to n do |
| > | MVc1[i]:=(m1*w*r*sum(cos(f[k]),k=i..n)); |
| > | end do; |
| > |
Таблица суммарного импульса остатка после отделения
| > | MVc2[0]:=0; |
| > | for i from 1 to n do |
| > | MVc2[i]:=(m1*w*r*sum(cos(f[k]),k=i..n-1)); |
| > | end do; |
| > |
Заполнение DS -таблицы значений расстояний: от ЦМ остатка до оси вращения M0, т.е до точки отделения частицы
| > | DS[0]:=0; |
| > | for i from 1 to n do |
DS[i]:=-r*m1*sum(sin(f[k]),k=i..n)/(M0+m1*(n-i)); (По мнению Василия - это неправильно)
| > | DS[i]:=-r*m1*sum(sin(f[k]),k=i..n)/(M0+m1*(n-i+1)); (Васино "исправление") |
| > | end do; |
| > |
Скорость изменения величины DS в момент предшествующий отделению i-ой дробинки
| > | VDS[0]:=0; |
| > | for i from 1 to n do |
VDS[i]:=-r*m1*w*sum(cos(f[k]),k=i..n)/(M0+m1*(n-i)); (По мнению Василия - это неправильно)
| > | VDS[i]:=-r*m1*w*sum(cos(f[k]),k=i..n)/(M0+m1*(n-i+1)); (Васино "исправление") |
| Конечно, каждый
имеет право считать что-либо правильным или неправильным... Но кричать об ошибке ?! Для этого надо быть очень "недалеким" человеком...
Это не ошибка.
Здесь представлены результаты расчета, как по
"красному" выражению, так и по "синему". |
| > | end do; |
Дельта дельты :)
| > | DD[0]:=0; |
| > | for i from 1 to n do |
| > | DD[i]:=-r*m1*sum(sin(f[k]),k=i..n-1)/(M0+m1*(n-i))+r*m1*sum(sin(f[k]),k=i..n)/(M0+m1*(n-i+1)); |
| > | end do; |
Стартовые значения
| > | V[0]:=0;Vc[0]:=0;Sc[0]:=0;S[0]:=0; CMc[0]:=0; CM[0]:=0; |
| > |
Цикл заполнения V[i],S[i],Vc[i],Sc[i],CM[i],CMc[i]
| > | for i from 1 to n do |
| > |
Скорость дробинки.
| > | V[i]:=Vc[i-1]+VDS[i-1]+w*r; |
Расстояние, пройденное дробинкой
| > | S[i]:=Sc[i-1]+DS[i-1]+V[i]*(n-i)*dt; |
Скорость остатка.
| > | Vc[i]:=(Vc[i-1]*(M0+m1*(n-i+1))-m1*V[i])/(M0+m1*(n-i)); |
| > |
Координаты центра масс остатка!
| > | Sc[i]:=Sc[i-1]+DD[i-1]+Vc[i]*dt; |
| > |
Координаты центра масс дробинок!
Вычисление должно быть похоже на вычисление S[i]
| > | CM[i]:=sum(Sc[k-1]+DS[k-1]+V[k]*(i-k+1)*dt,k=1..i)/i; |
Координаты центра масс всей системы!
| > | CMc[i]:=(m1*i*CM[i]+(M0+m1*(n-i))*Sc[i])/(M0+m1*n); |
| > | end; |
| > |
конец процедуры
| > | end: |
| > |
Объявление процедуры Jet - расчет для системы с реактивным отделением
Здесь все, практически, то же самое.
Величины такие же, помечены буквой "j".
Разумеется, отсутствуют величины: DD, DS, VDS.
| > | Jet:=proc(n) |
| > | global Vj,Sj,Vcj,Scj,dt,CMcj,CMj; |
| > |
| > |
| > | dt:=2*Pi/(w*n); |
| > | m1:=M1c/n; |
| > |
| > | Vj[0]:=0;Vcj[0]:=0;Scj[0]:=0;Sj[0]:=0;CMcj[0]:=0; CMj[0]:=0; |
| > |
Цикл заполнения Vj[i],Sj[i],Vcj[i],Scj[i],CMj[i],CMcj[i]
| > | for i from 1 to n do |
Скорость дробинки.
| > | Vj[i]:=Vcj[i-1]+w*r; |
Расстояние, пройденное дробинкой
| > | Sj[i]:=Scj[i-1]+Vj[i]*(n-i)*dt; |
Скорость ЦМ остатка .
Я просто беру суммарный импульс летящих дробинок. Импульс остатка равен этой величине.
Делим на массу - получаем скорость!
| > | Vcj[i]:=-(m1*sum(Vj[k],k=1..i))/(M0+m1*(n-i)); |
| > |
Координаты Центра Масс остатка!
| > | Scj[i]:=Scj[i-1]+Vcj[i]*dt; |
Координаты Центра Масс дробинок!
| > | CMj[i]:=sum(Scj[k-1]+Vj[k]*dt*(i-k+1),k=1..i)/i; |
Центр масс всей системы!
| > | CMcj[i]:=(m1*i*CMj[i]+(M0+m1*(n-i))*Scj[i])/(M0+m1*n); |
| > | end; |
| > |
| > | end:#конец процедуры Jet |
| > |
Начало расчета
Количество "дробинок"
| > | n:=22; |
![]()
| > |
"оцифровка" переменных.
Необходима для построения графиков
r -радиус центрифуги
w -угловая скорость вращения центрифуги
M1c -суммарная масса дробинок, находящихся в каждой системе
M0 -масса пустого корпуса каждой системы
| > | r:=1;w:=1;M1c:=1;M0:=10; |
![]()
![]()
![]()
![]()
| > |
Вызов функций
| > | Non_jet(n): |
| > | Jet(n): |
| > |
| > |
Результаты расчетов :
| > |
| > | #================================================================================================= |
Графики относительных смещений "Дельта" и "Дельта-дельты"
| > | PDD:=[[Time[i],DD[i]] $i=0..n]: # набор для графика DD (дельта дельты) |
| > | PDS:=[[Time[i],DS[i]] $i=0..n]:# набор для графика DS (дельты) |
| > | plot(PDD,x=dt..2*Pi/w,title="Дельта дельты для (M0+m1*(n-i+1)"); |
| > | plot([PDS,PDD],x=dt..2*Pi/w,title="Большая кривая - смещение 'дельта', малая - 'дельта дельты', для (M0+m1*(n-i+1)",axes=frame,legend=["дельта DS","дельта дельты DD"]); |
![[Maple Plot]](images22_2/22shots_26.gif)
![[Maple Plot]](images22_2/22shots_27.gif)
![[Maple Plot]](images22_2/22shots_28.gif)
![[Maple Plot]](images22_2/22shots_29.gif)
Почему здесь представлены 2 рисунка?
В первом полупериоде, расстояние DS положительно и возрастает.
| > | #================================================================================================= |
График относительной скорости перемещения оси вращения (точки отделения дробинок) относительно ЦМ остатка .
| > | PVDS:=[[Time[i],VDS[i]] $i=0..n]:# набор для графика относительной скорости VDS |
| > | plot(PVDS,t=dt..2*Pi/w,title="График относительной скорости VDS для (M0+m1*(n-i+1)"); |
| > |
![[Maple Plot]](images22_2/22shots_210.gif)
![[Maple Plot]](images22_2/22shots_211.gif)
Почему здесь представлены 2 рисунка?
В первом полупериоде, скорость VDS положительна.
И направление совпадает с направлением движения оторвавшейся дробинки!
| > |
| > |
| > |
| > | #================================================================================================= |
Sc и Scj - координаты ЦМ "остатка". Данный график иллюстрирует изменение этих координат со временем.
| > | PScj:=[[Time[i],Scj[i]] $i=0..n]:# набор для графика положения ЦМ остатка при реактивном движ. |
| > | PSc:=[[Time[i],Sc[i]] $i=0..n]:# набор для графика того же самого для центрифуги. |
| > | plot([PSc,PScj],t=0..2*Pi/w,title="Перемещение ЦМ остатков для (M0+m1*(n-i+1)",legend=["ЦМ остатка центриф","ЦМ остатка реактив"]); |
![[Maple Plot]](images22_2/22shots_212.gif)

Почему здесь представлены 2 рисунка?
| > | #================================================================================================ |
График "цепочек" дробинок, т.е. положение дробинок в момент окончания цикла.
| > | PSj:=[[Sj[n-j],j] $j=0..n-1]:# набор для графика положения дробинок (реактивное движ) |
| > | PS:=[[S[n-j],j] $j=0..n-1]:# набор для графика положения дробинок (центрифуга) |
| > | plot([PS,PSj,PS,PSj],s=S[n]..S[1],title="Положение дробинок в момент окончания цикла.( Временной срез) для (M0+m1*(n-i+1)", labels=["расстояние от точки старта в момент времени t=2Pi/w","Номер дробинки"],legend=["цепочка от центрифуги","цепочка от реактив"," "," "],style=[line,line,point,point],color=[red,blue,red,blue],symbol=circle,symbolsize=5); |
![[Maple Plot]](images22_2/22shots_213.gif)
![[Maple Plot]](images22_2/22shots_214.gif)
Почему здесь представлены 2 рисунка?
| > | #================================================================================================ |
Графики перемещения Центров масс всех компонентов систем
| > |
| > | PCMj:=[[Time[j],CMj[j]] $j=0..n]:# набор для графика Центра масс цепочек дробинок при "обычном" реактивном. |
| > | PCM:=[[Time[j],CM[j]] $j=0..n]:# набор для графика того же самого для центрифуги |
| > |
| > | plot([PSc,PScj,PCM,PCMj],t=0..2*Pi/w,title="Нижняя часть графика-перемещение ЦМ остатка,верхняя- перемещение ЦМ цепочки дробинок для (M0+m1*(n-i+1)",legend=["ЦМ остатка центрифуги","ЦМ остатка реактив","ЦМ шлейфа центриф","ЦМ шлейфа реактив"],color=[red,green,brown,blue]); |


Почему здесь представлены 2 рисунка?
Две кривые в нижней части графика совпадают.
Это графики перемещения Центров Масс корпусов с остатками груза.
| > | #================================================================================================ |
| > |
Этот график - "верхняя часть" предыдущего графика, где собраны 4 кривые.
| > |
Подчеркну: CM и CMj - это именно центры масс цепочек дробинок в каждый момент времени.
| > | plot([PCM,PCMj],t=0..2*Pi/w,title="Перемещения ЦМ дробинок в течение рабочего периода для (M0+m1*(n-i+1)",legend=["ЦМ шлейфа выброса центрифуги","ЦМ шлейфа выброса реактив"]); |
![[Maple Plot]](images22_2/22shots_217.gif)
![[Maple Plot]](images22_2/22shots_218.gif)
Почему здесь представлены 2 рисунка?
| > | #================================================================================================ |
Специальное построение графика,на котором видно изменение плотности распределения частиц груза в цепочках выброса.
| > | PSj:=[[Sj[n-j],0] $j=0..n-1]:# набор для условного графика реактив. |
| > | PS:=[[S[n-j],0.1] $j=0..n-1]:# набор для условного графика центриф. |
| > | plot([PS,PSj,[[0,1],[S[1],1]],[[0,-1],[S[1],-1]]],S=0..S[1],title="Визуализация распределения дробинок в цепочке для (M0+m1*(n-i+1)",style=point,axes=none,scaling=unconstrained,legend=["центрифуга","реактив","_","_"],color=[red,blue,white,white],symbol=circle,symbolsize=5);# |
![[Maple Plot]](images22_2/22shots_219.gif)
![[Maple Plot]](images22_2/22shots_220.gif)
Почему здесь представлены 2 рисунка?
| > | #================================================================================================ |
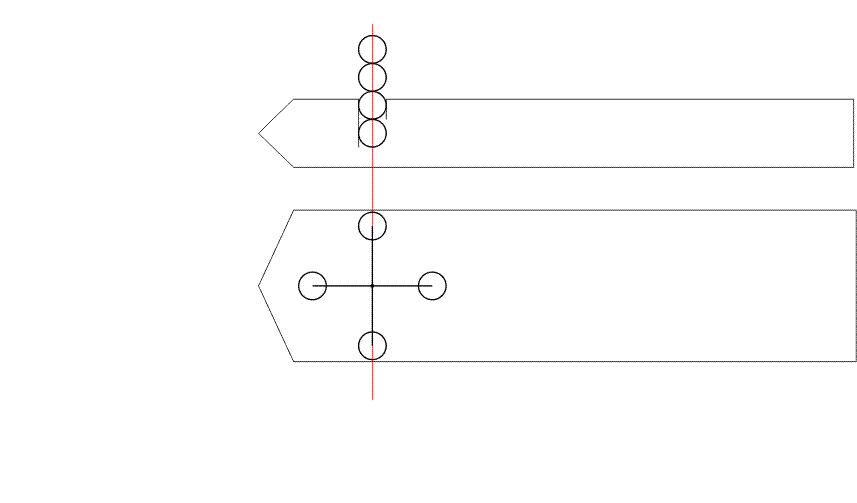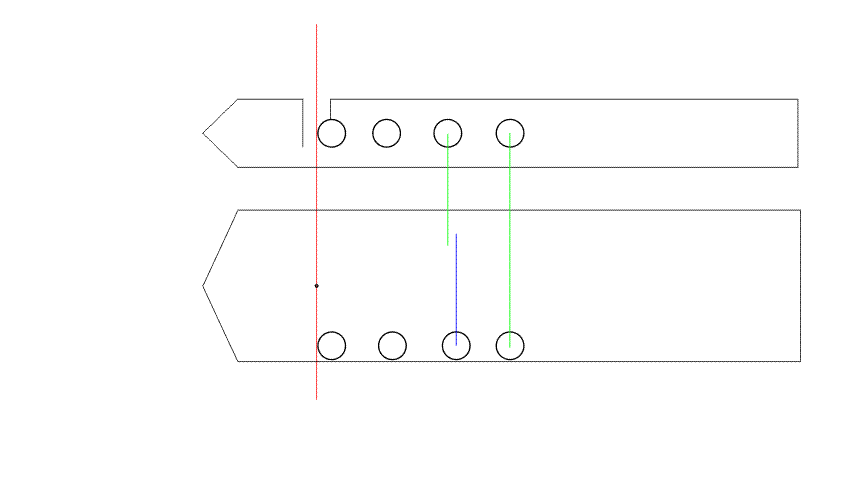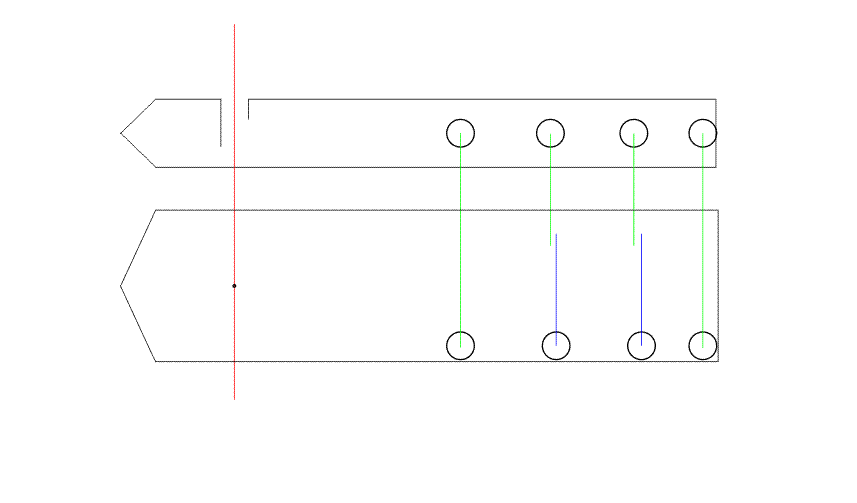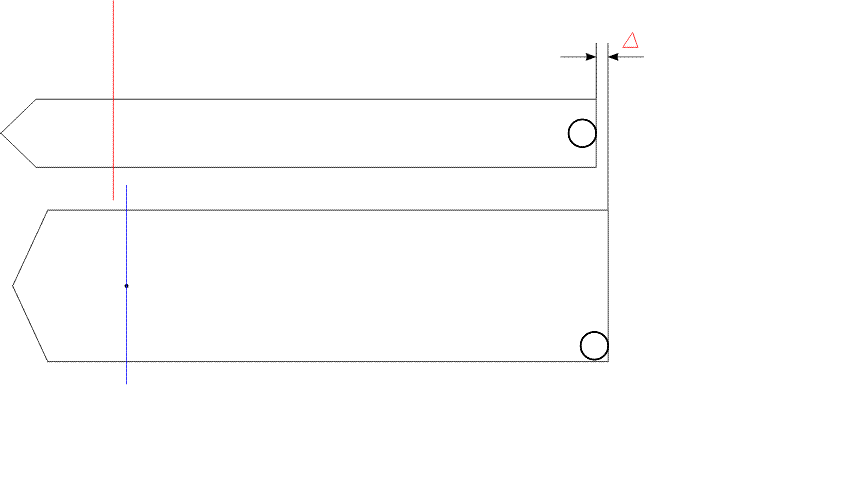
График траекторий дробинок
DS[0] DS -таблицы значений расстояний: от ЦМ остатка до оси вращения M0, т.е до точки отделения частицы
Sc[i] Координаты центра масс остатка!
S[i] Расстояние, пройденное дробинкой
| > |
| > | PScDs:=[[[Sc[j]+DS[j],n-j+1],[S[j],0]] $j=1..n ]:#набор для графика движения дробинок not_jet. |
| > | Pl1:=plot(PScDs,s=S[1]..S[n],color=red): |
| > |
| > | PScDsj:=[[[Scj[j],n-j+1],[Sj[j],0]] $j=1..n ]:#набор для графика движения дробинок jet. |
| > | Pl2:=plot(PScDsj,s=S[1]..S[n],color=blue,linestyle=DASH): |
| > | Pl_axe_X0:=plot([[0,n],[0,0]],color=green): |
| > | display([Pl1,Pl2,Pl_axe_X0],axes=frame,title="График траекторий отделяющихся дробинок. Красный цвет- центрифуга, синий - реактивное отделение для (M0+m1*(n-i+1)");#,legend=["центрифуга","реактив"]); |
| > |
![[Maple Plot]](images22_2/22shots_221.gif)
![[Maple Plot]](images22_2/22shots_222.gif)
Почему здесь представлены 2 рисунка?
| > | #================================================================================================ |
График абсолютных скоростей дробинок в цепочках выбросов.
| > | PVj:=[[j,Vj[j]] $j=1..n]:# набор для графика изменения скоростей реактив. |
| > | PV:=[[j,V[j]] $j=1..n]:# набор для графика изменения скоростей центриф. |
| > | plot([PV,PVj],number=1..n,title="Абсолютные скорости дробинок для (M0+m1*(n-i+1)", legend=["центрифуга","реактив"],color=[red,blue]);# |
![[Maple Plot]](images22_2/22shots_223.gif)
![[Maple Plot]](images22_2/22shots_224.gif)
Почему здесь представлены 2 рисунка?
| > | #================================================================================================ |
График, иллюстрирующий изменение скоростей дробинок в цепочке выброса.
Т.е. разница в скоростях последующей "дробинки" от предыдущей.
| > | PDVj:=[[j,evalf(Vj[j+1]-Vj[j])] $j=2..n-1]:# набор для графика изменения скоростей реактив. |
| > | PDV:=[[j,V[j+1]-V[j]] $j=2..n-1]:# набор для графика изменения скоростей центриф. |
| > | plot([PDV,PDVj],t=2..n-1,title="Изменение скоростей дробинок для (M0+m1*(n-i+1)",legend=["центрифуга","реактив"],color=[red,blue]);# |
![[Maple Plot]](images22_2/22shots_225.gif)
![[Maple Plot]](images22_2/22shots_226.gif)
Почему здесь представлены 2 рисунка?
| > | #================================================================================================ |
График, иллюстрирующий изменение скоростей Центров масс цепочек дробинок и ЦМ остатков [корпус+остаток груза]
| > | PVCMj:=[[Time[j],(CMj[j+1]-CMj[j])/dt] $j=1..n-1]:# набор для графика изменения скоростей реактив. |
| > | PVCMcj:=[[Time[j],(CMcj[j+1]-CMcj[j])/dt] $j=1..n-1]:# набор для графика изменения скоростей реактив. |
| > | PVCM:=[[Time[j],(CM[j+1]-CM[j])/dt] $j=1..n-1]:# набор для графика изменения скоростей центриф. |
| > | PVCMc:=[[Time[j],(CMc[j+1]-CMc[j])/dt] $j=1..n-1]:# набор для графика изменения скоростей центриф. |
| > | plot([PVCM,PVCMj],t=dt..2*Pi/w,title="Изменение скоростей ЦМ дробинок для (M0+m1*(n-i+1)",legend=["шлейф центрифуга","шлейф реактив"],color=[red,blue]);# |
| > | plot([PVCMc,PVCMcj],t=dt..2*Pi/w,title="Изменение скоростей ЦМ остатков для (M0+m1*(n-i+1)",legend=["остаток центриф","остаток реактив"],color=[red,blue],axes=frame);# |
![[Maple Plot]](images22_2/22shots_227.gif)
![[Maple Plot]](images22_2/22shots_228.gif)
Почему здесь представлены 2 рисунка?
![[Maple Plot]](images22_2/22shots_229.gif)
![[Maple Plot]](images22_2/22shots_230.gif)
Почему здесь представлены 2 рисунка?
| > | #================================================================================================ |
Здесь представлена разность двух кривых с графика "Изменение скоростей ЦМ дробинок"
| > | PDCM:=[[Time[j],CM[j]-CMj[j]] $j=0..n]:# набор для графика разницы в положении ЦМ цепочек дробинок. |
| > | plot(PDCM,t=dt..2*Pi/w,axes=frame,title="Разница в положении ЦМ цепочек дробинок с течением времени для (M0+m1*(n-i+1)"); |
![[Maple Plot]](images22_2/22shots_231.gif)
![[Maple Plot]](images22_2/22shots_232.gif)
Почему здесь представлены 2 рисунка?
| > | #=============================================================================================== |
График координат ЦЕНТРОВ МАСС систем за рабочий период
| > | PCMcj:=[[Time[j],CMcj[j]] $j=0..n]:# набор для графика ЦМ всей реактивной системы |
| > | PCMc:=[[Time[j],CMc[j]] $j=0..n]: # набор для графика ЦМ системы с центрифугой |
| > | plot([PCMc,PCMcj],t=dt..2*Pi/w,axes=frame,title="Положение ЦМ всех систем для (M0+m1*(n-i+1)",legend=["ЦМ Центрифуга","ЦМ реактив"],style=[line,line]); |
![[Maple Plot]](images22_2/22shots_233.gif)
![[Maple Plot]](images22_2/22shots_234.gif)
Почему здесь представлены 2 рисунка?
| > | #============================================================================================== |
Проверка!
Проверка заключается в вычислении суммарного импульса системы с центрифугой.
Рассчитывается импульс "остатка" через скорость ЦМ, и импульс, как сумма импульсов всех компонентов, входящих в "остаток".
Эти величины сравниваются с суммарным импульсом цепочки "дробинок".
| > | m1:=M1c/n: |
Абсолютная скорость оси центрифуги:
| > | for i from 0 to n do |
| > | Vos[i]:=Vc[i]+VDS[i]; |
| > | end do: |
Импульс остатка, как сумма импульсов компонентов системы:
| > | for i from 0 to n do |
| > | Qost[i]:=MVc1[i]+Vos[i]*((n-i)*m1+M0); |
| > | end do: |
Количество движения цепочки дробинок:
| > | for i from 0 to n do |
| > | Qdr[i]:=m1*sum(V[k],k=0..i); |
| > | end do: |
| > |
Импульс остатка через скорость ЦМ:
| > | for i from 0 to n do |
| > | Qcm[i]:=Vc[i]*(M0+m1*(n-i)); |
| > | end do: |
| > |
| > | PQost:=[[Time[j],Qost[j]] $j=0..n]: |
| > | PQdr:=[[Time[j],Qdr[j]] $j=0..n]: |
| > | PQcm:=[[Time[j],Qcm[j]] $j=0..n]: |
| > | Psumm:=[[Time[j],Qost[j]+Qdr[j]] $j=0..n]: |
| > | plot([PQost,PQdr,PQcm,Psumm],t=0..2*Pi/w,title="Импульсы компонентов системы с центрифугой для (M0+m1*(n-i+1)",legend=["Импульс остатка через сумму импульсов компонентов","Импульс летящих дробинок","Импульс остатка через скорость ЦМ","сумма"],color=[red,green,brown,blue],style=[line,line,point,line],symbol=circle,symbolsize=5); |
![[Maple Plot]](images22_2/22shots_235.gif)
![[Maple Plot]](images22_2/22shots_236.gif)
Почему здесь представлены 2 рисунка?
| > |
График суммарного импульса системы
| > | plot(Psumm,t=dt..2*Pi/w,title="Сумма для (M0+m1*(n-i+1)",color=blue); |
![[Maple Plot]](images22_2/22shots_238.gif)
| Конечно, каждый
имеет право считать что-либо
правильным или неправильным... Но кричать об ошибке ?! Для этого надо быть очень "недалеким" человеком...
Результат, получаемый при
использовании "красного"
выражения выявляет погрешность ~10-3
(и эта погрешность уменьшается при увеличени числа "шагов"), |
Нормальные расчеты можно посмотреть здесь