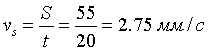|
|
||||||||||||||||||||||||||||||||||||||||||||
Comparative parameters of the motion:
Work:
Kinetic energy
They are obtained from the latter by the formal replacement of m → I , v → w , p → L The represented table cannot pretend to full weight of the scope of analogous values. For rotatory and forward motions are formulated the analogous laws:
These laws are formulated as follows:
In the classical mechanics the law of momentum
conservation usually is derived as the consequence of Newton's law. However,
this law of conservation is accurate in cases when Newtonian mechanics is not
applied (relativistic physics, quantum mechanics). It can be obtained as the
consequence of intuitive- accurate assertion about the fact that the properties
of our peace will not change, if all its objects (or reference point!) to move
for the certain vector
R. At present there does not exist any experimental facts, which
testify about the non fulfillment of the law of momentum conservation. Given laws relate to the global laws of conservation.
...4. Turning to the proof of the law of momentum conservation. Let us assume that the mechanical system is locked. All forces F1 , F2 ..., the acting on the material points systems, are forces internal, there are no external forces. Let us transfer system from arbitrary position 1 to another arbitrary position 2 so that all its material points would undergo one and the same displacement r, and besides so that their speeds would remain before in the value and the direction. In view of the uniformity of space, to this displacement does not be required the expenditures of work. But this work is the scalar product (F1 + F2 +...)r . It means, it is equal to zero, whatever displacement r. Hence it follows that for the closed system F1 +F2 +... of =0. A this is the very thing condition, with fulfilling of which of second Newton's law is obtained the law of momentum conservation. 5. The law of conservation of momentum of pulse for the closed system proves exactly so. Using isotropy of space, it is possible to prove that the vector sum of the moments of the internal forces, which act in the system, is equal to zero: M1 +M2 +... =0. hence immediately follows the law in question. As is evident, proofs are very similar.With the entire similarity of progressive and rotary motion, they have differences. One of them is examined in this article. There is a phenomenon, which enters, it would seem, in the contradiction with LCMP.
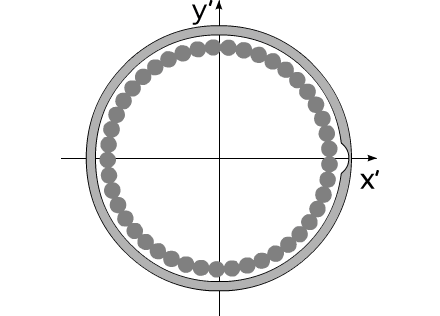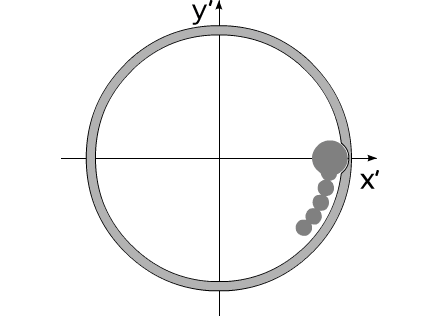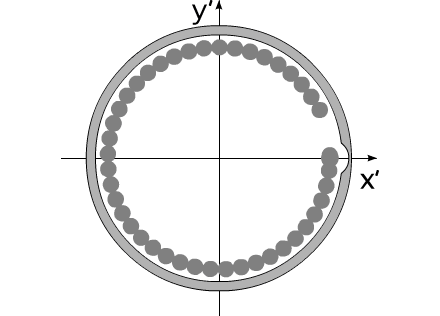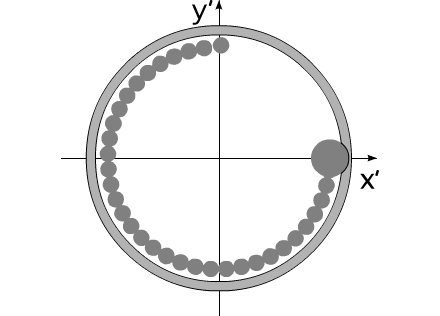
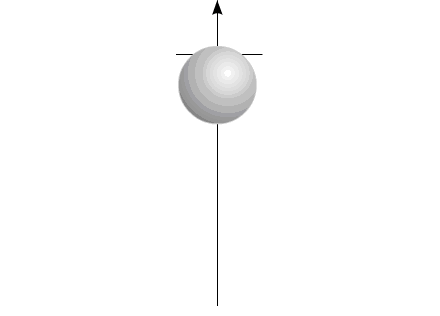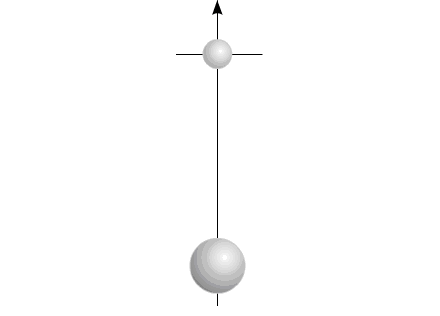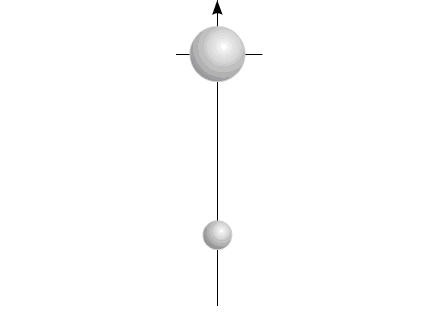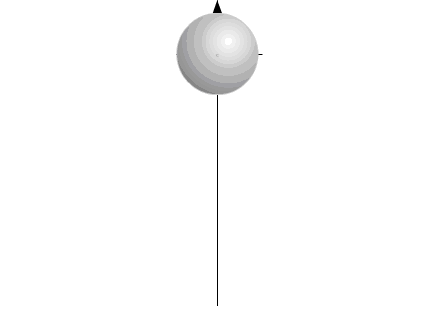
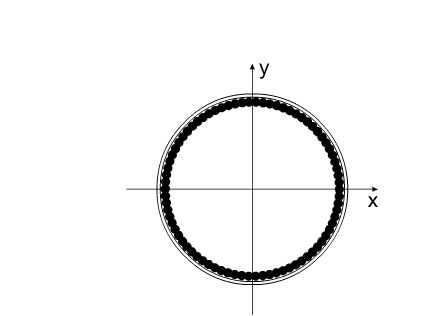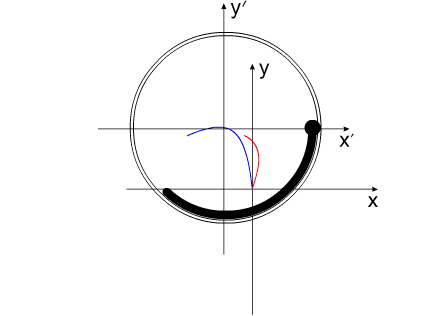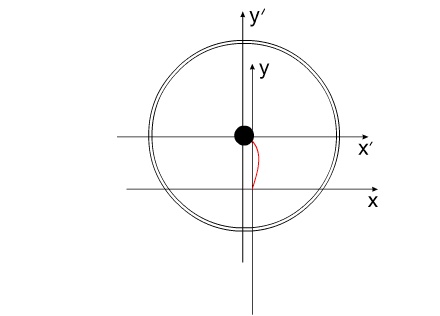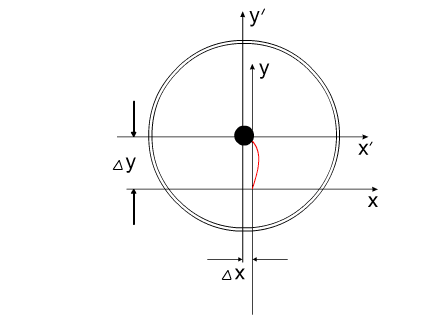
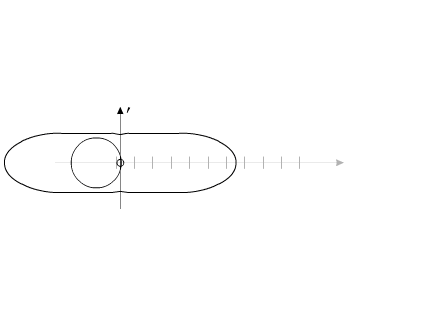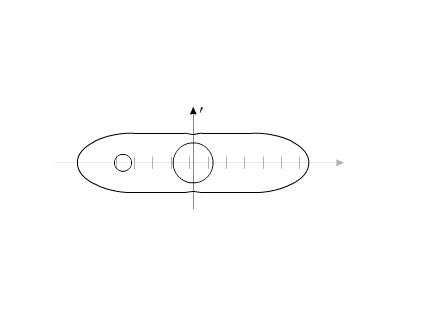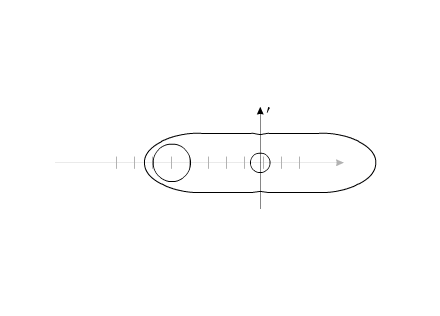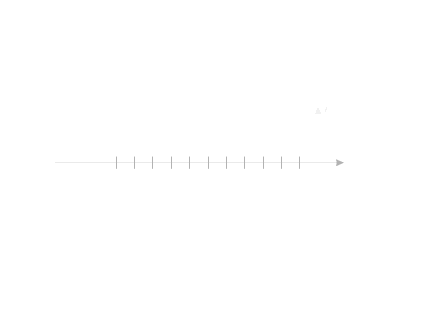
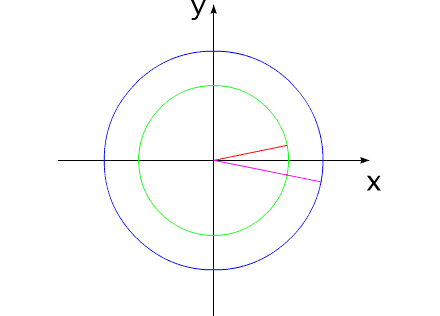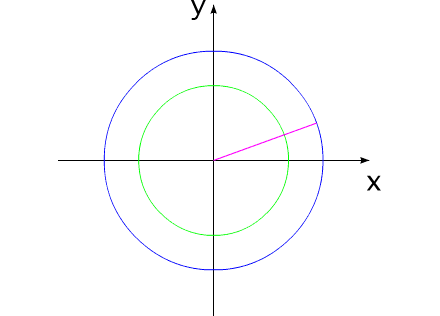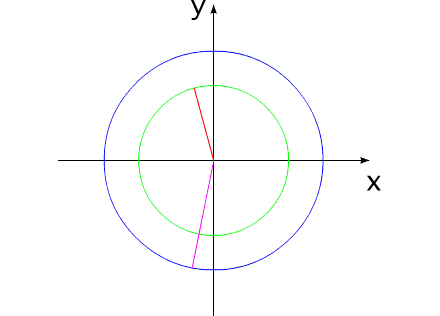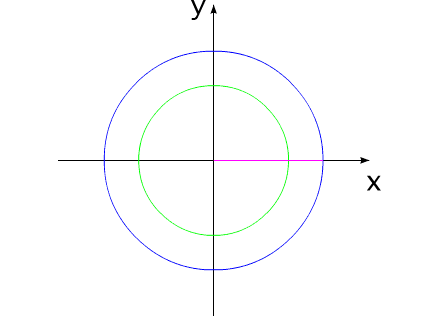
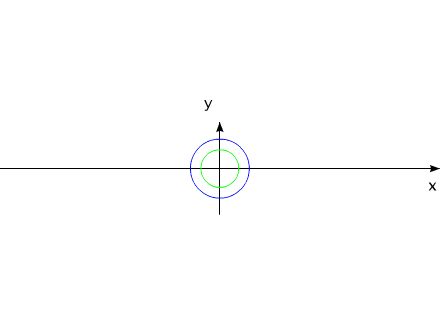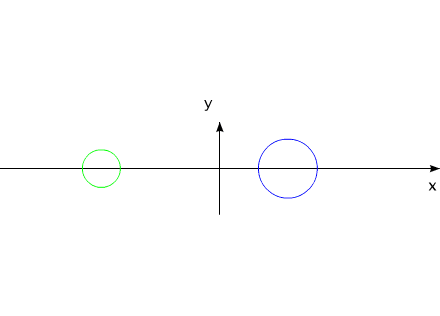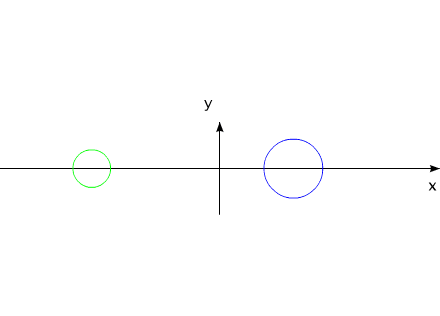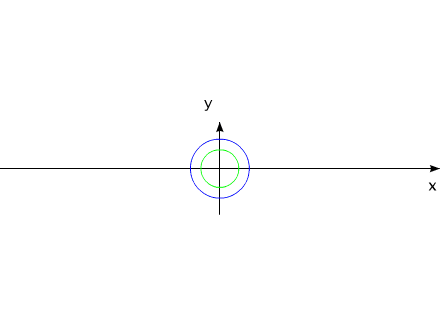
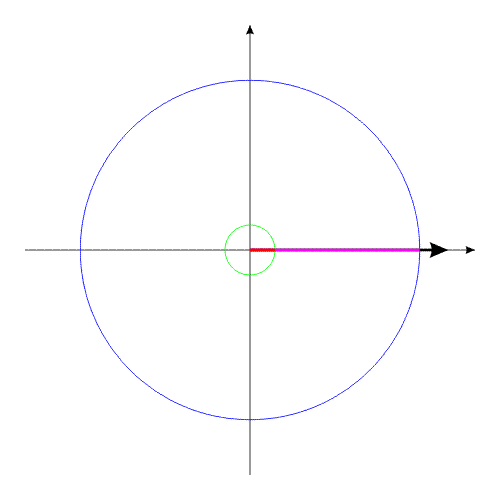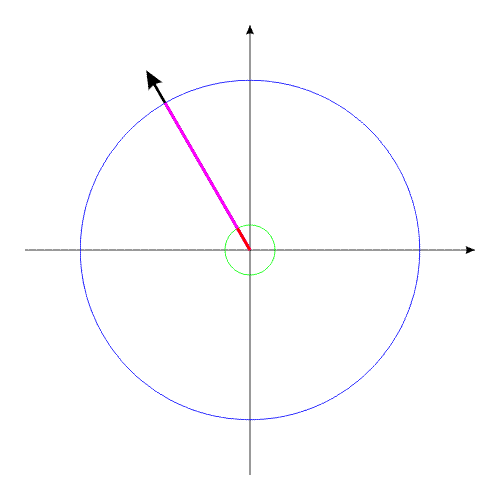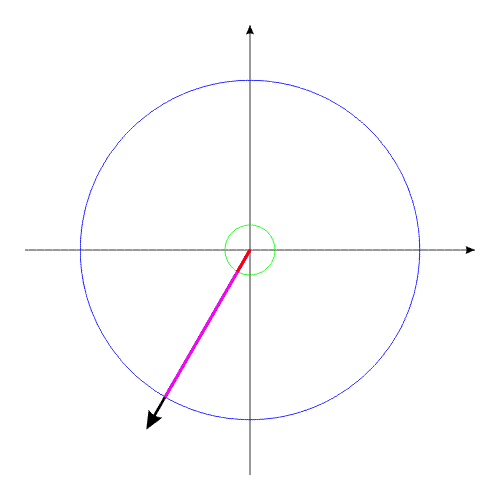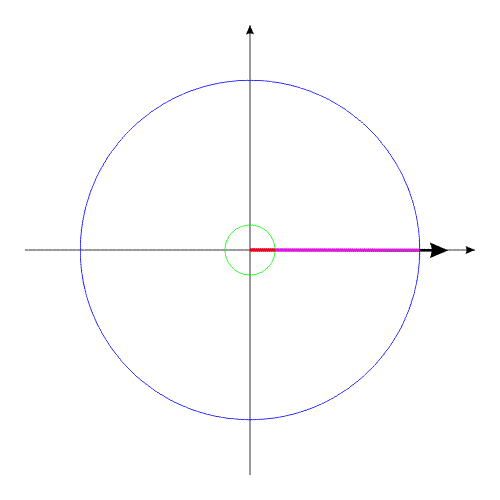
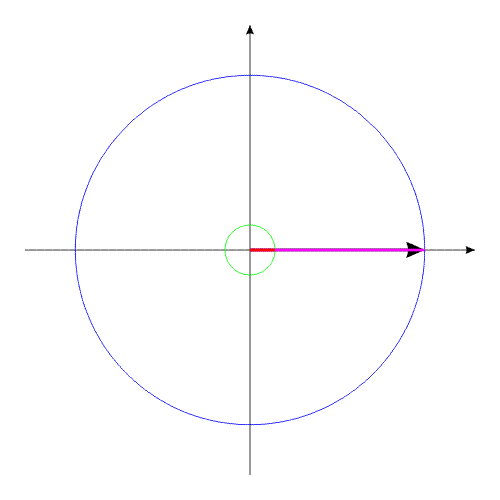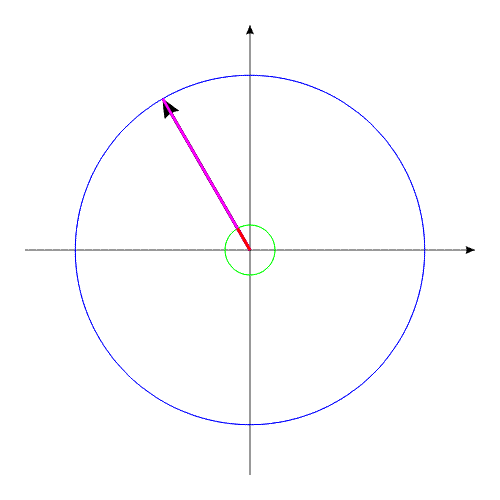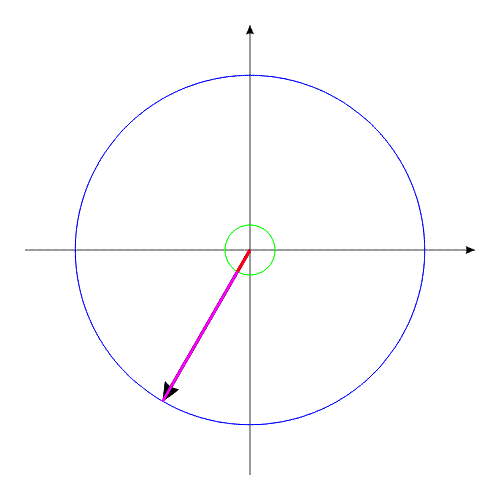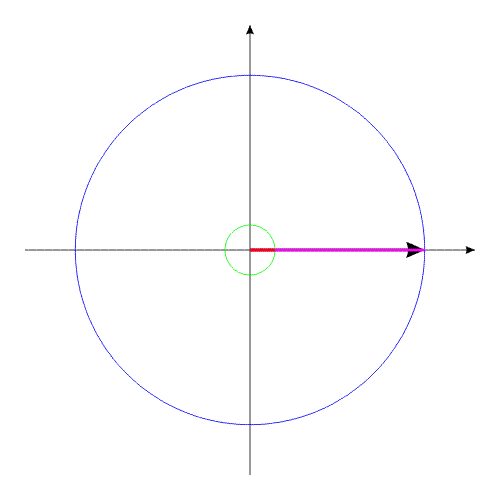
How it is possible to turn mechanical system with the aid of some internal forces alone? Let us examine an example. Let us assume we have two balanced bodies, fixed coaxially. Bodies have the capability to revolve relative to each other. One of the bodies (green outline, a red radius) is capable of changing its geometric dimensions, changing, thus, its moment of inertia (Iv). Let us assume the maximum value of Iv max of this body corresponds to value of Ic of the second body (dark-blue outline, a purple radius). The minimum value of Iv min is considerably lower than Iv max. Let us examine the cycle of motions of this mechanical system. Fig.1 Body with by variable Iv acquires maximum geometric sizes. (due to the internal energy, it understands).Due to the same internal energy let us create the internal torque, which acts equally on both bodies. Under the action of this moment, body they begin to be turned in opposite directions. It is possible to stop motion of both bodies at any moment of time. Since the moments of inertia of both bodies are equal, angular positions both bodies will engage identical (in the absolute value). At the moment of stop, the angular position of entire system remained before. Will not change this angular position and when we will begin to change geometric dimensions of one of the bodies. After decreasing the geometric dimension, and respectively the moment of inertia of one of the bodies, let us try to reduce both bodies to the previous angular positions of these bodies, with the aid of the power moment, directed to other side. Here and occurs interesting. Since the moments of inertia of both bodies are
already different, both bodies it is turned to the different angles. It is
possible to again increase dimensions of one of the bodies. System will again be
such as before. These cycle of motions can be repeated. Fig.2 Moreover, it revolves entirely well!Let us assume the components of system change their geometric dimensions in such a way that total moment of the inertia of entire system remains without the changes. Depicted on fig3 system can be examined as interaction of bodies with the variable torque of inertia, with the constant mass and constant moment of the inertia of entire system as a whole. Fig.3 The system, as shown in animated
fig3, accomplishes the complete revolution in 16
seconds.
But, in reality, it cannot be spoken about this value as about the "speed of rotation of system". More right it will sound: the "rate of the process of changing the angular position", since value wφ it is not the measure of the kinetic state of this system, since kinetic energy of system does not change. The motion examined is inertia-free. If we stop the relative displacements of components inside the closed system, motion wφ immediately it ceases. To value wφ most of all approaches name precession. In the process of a similar "rotation" is not disrupted LCMP, since total moment of momentum of all components of system, at each moment of time, is equal to zero. At the same time it is possible to determine the moment of force, equivalent to the external moment of force, which should have been applied to the system in order to cause a similar displacement. Specifically, - equivalent, since for the situation in question, the external power moment is equal to zero. The conclusions, which can be made on the basis of the given example:
Let us return to the proofs LMC and LCMP on the basis of the property of the symmetry of space. Proofs are constructed on the assumption of a certain displacement of system (turning, in the case LCMP). But in the case of the revolving system, this displacement actually can be produced due to the internal energy. I.e., displacement not is virtual, but it is completely actual. In the large table of analogous expressions for the rotatory and progressive displacements, appears the large empty cell:
Displacement due to the internal forces? In the case with the progressive
displacement, such it seems inadmissibly. On this score even there is a "theorem
about the motion of the center of masses", which, it is at first glance, does
not allow the similar displacement:
This expression is obtained as a result of the formal replacement φ→S , M→F , L→p
VaripendThe properties of mechanical system, by the name "varipend", most fully satisfy the enumerated assumptions.
Fig.4 Name "varipend" is obtained from the confluence of two words:
varipend =variable +pendulum .
Fig.5 Or, in the projection on one coordinate:
Fig.6 The changing size of components in the figure symbolizes a
change in the mass of the elements of the system:
In one of the calculations of the displacement of "varipend" is
used the equation of motion of the body of variable mass - equation of Meshcherski'y.
Fig.7
Fig.8 It is possible to conduct analogy with figure 3.System, depicted on fig.8, are moved up to the distance of 55 mm in 20 seconds. It would seem, it is possible to calculate the speed of "varipend":
But, since in the process of displacement the total impulse of system remains
constant, value vs
will be formal value, which determines only changes in the coordinates of the
centre of masses. This value is in no way connected with the pulse of entire
system. |
||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||
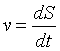
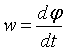
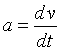
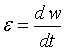
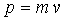
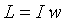
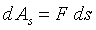
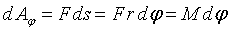
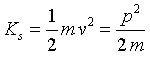
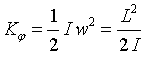
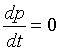 ,
with Fext
= 0
,
with Fext
= 0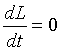 ,
with Mext
= 0
,
with Mext
= 0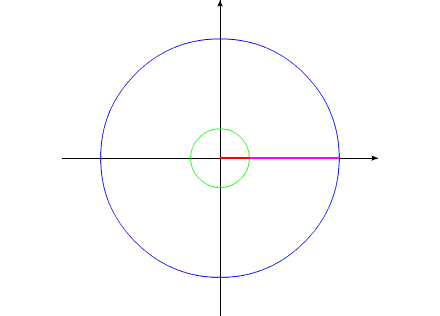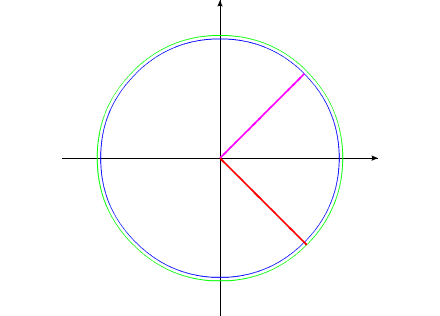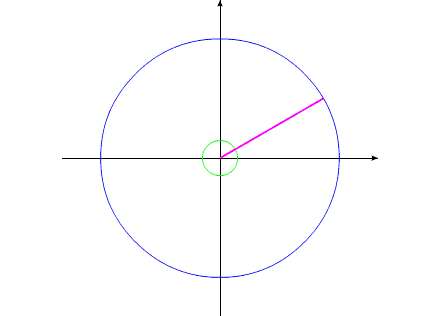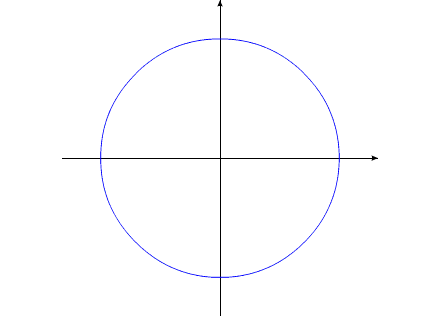
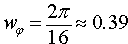 rad/s
rad/s