|
комментарий к статье "Аналогия между
вращательным и поступательным движениями"
Такой, с позволения сказать, «закон» невозможно сформулировать и доказать. Попытка сформулировать этот «закон» сразу же войдет в противоречие с Первым законом Ньютона: «материальная точка (или Центр Масс замкнутой механической системы) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не выведет ее из этого состояния». А доказать «неподвижность замкнутой механической системы без внешнего воздействия» невозможно вот по какой причине: В общем случае, для сложной механической системы (т.е., для системы с числом взаимодействующих тел 3 и более), поведение ЦМ – неопределённо. Для механической системы из трех и более тел, уравнение движения центра масс такой системы может иметь такой вид:
где:
Для механической системы из трех и более тел уравнение движения центра масс не имеет общего решения! (В том числе, при нулевых начальных условиях.)
Решению этого уравнения удовлетворяет бесконечное множество траекторий ЦМ, лежащих в некоторой области внутри замкнутой механической системы. При сохранении суммарного импульса системы. Траекторий! Точка с координатами «0,0,0» - только один частный случай из бесконечного множества траекторий!
Это дифференциальное уравнение
может решаться только для частных случаев, то есть,
накладывая те или иные ограничения на свойства и условия
взаимодействий компонентов системы (т.е. зная функции
Одним из таких частных случаев является случай взаимодействия двух тел (или сводя все взаимодействия замкнутой механической системы к взаимодействию двух тел).
Но распространять одно частное решение на все случаи взаимодействий в любых изолированных механических системах, является грубой ошибкой. От «частного» нельзя перейти к
«общему».
1. ЦМ – это просто геометрическая координата. Результат математической функции. Функция координат ЦМ может иметь такой вид: Rc(t)=const(t) Так описывается безынерционное перемещение.
Выражение: определяет
радиус-вектор ЦМ механической системы, состоящей из 2
(двух) тел.
Все взаимодействия внутри изолированной механической системы сводятся к взаимодействию двух тел согласно парности всех сил в соответствии с Третьим законом Ньютона: "Тела действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению":
Выражение (1) определяет координаты точки C0 , в которую может быть собрана (стянута) вся механическая системы с помощью всех парных взаимодействий внутри этой механической системы. Равенство "Нулю" радиус-вектора ЦМ возможно при "нулевых" начальных условиях, т.е. при начальной скорости, ускорении и начальных координатах ЦМ, равных нулю.
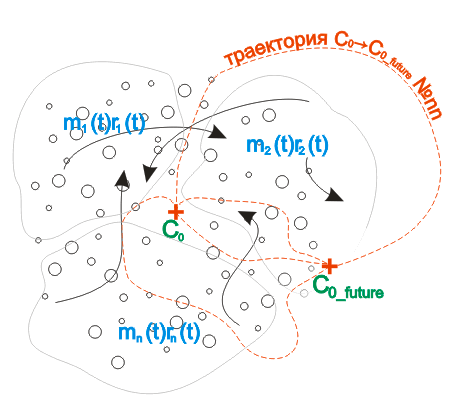
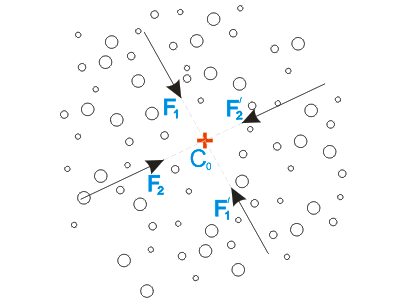
В то же время, выражение для радиус-вектора ЦМ сложной механической системы:
говорит о том, что координаты ЦМ, с течением времени, могут быть "любыми" (Рис.2).
C
помощью выражения (1): Но мы не можем, не имеем
права, утверждать, что ЦМ сложной механической системы всегда, в
любой момент времени, будет находиться в точке
C0
. При этом, траектория
перемещения к точке
C0_
future
может быть любая (условие: неразрывная и непрерывная) . И таких
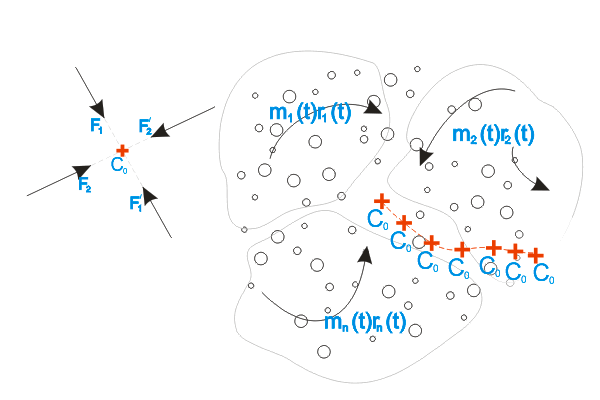
траекторий может быть неограниченное количество. Но в любой момент времени, к любой механической системе может быть применен метод (1), определяющий частное решение координат ЦМ:
Т.е., применяя третий закон Ньютона,
используя парные взаимодействия, мы можем стянуть всю систему в
точку
C0
Собственно, именно такой "набор точек C0" и представляет собой траекторию безынерционного перемещения механической системы Varipend (Варипенд).
Набор точек "возможного стягивания в
точку
C0
"...
Статья "Аналогия между вращательным и поступательным движениями" С.Бутов |
|
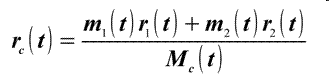 , при
, при
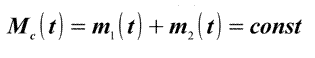
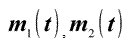 - массы
компонентов
- массы
компонентов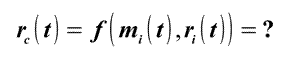
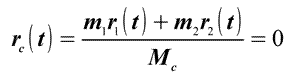
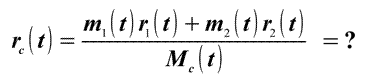 (2)
(2)