20 декабря 2012 г
В редакцию журнала "Прикладная
математика и механика".
Здравствуйте!
Прошу рассмотреть возможность
публикации моего материала в вашем издании.
Материал относится к
Теоретической механике.
Представляет собой задачу и несколько решений этой задачи.
Задача и ее решения доказывают возможность перемещения изолированной
механической системы только с помощью внутренних взаимодействий, без внешнего
воздействия.
Пожалуйста! Не торопитесь...
Очень
кратко, тезисно:
В физике, в разделе "Механика", никогда не существовало закона (теоремы, постулата, аксиомы и т.д.), который бы строго-настрого запрещал перемещаться замкнутой механической системе только с помощью внутренних взаимодействий. |
Такой, с позволения сказать, «закон» невозможно сформулировать и доказать.
Попытка сформулировать этот «закон» сразу же войдет в противоречие с Первым законом Ньютона:
«материальная точка (или Центр Масс замкнутой механической системы) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не выведет ее из этого состояния».
А доказать «неподвижность замкнутой механической системы без внешнего воздействия» невозможно вот по какой причине:
В общем случае, для сложной механической системы (т.е., для системы с числом взаимодействующих тел 3 и более), поведение ЦМ – неопределённо.
Для механической системы из трех и более тел, уравнение движения центра масс такой системы может иметь такой вид:
, при
где:
-
радиус вектор ЦМ
,
- радиус векторы ЦМ компонентов
,
- массы компонентов
- суммарная масса взаимодействующих компонентов.
Для механической системы из трех и более тел уравнение движения центра масс не имеет общего решения! (В том числе, при нулевых начальных условиях.)
Что скрывается за знаком вопроса в общем уравнении движения центра масс?
Решению этого уравнения удовлетворяет бесконечное множество траекторий ЦМ, лежащих в некоторой области внутри замкнутой механической системы. При сохранении суммарного импульса системы. Траекторий! Точка с координатами «0,0,0» - только один частный случай из бесконечного множества траекторий!
Это дифференциальное
уравнение может решаться только для частных случаев, то есть, накладывая
те или иные ограничения на свойства и условия взаимодействий компонентов системы
(т.е. зная функции
,
и опираясь на законы сохранений).
Говоря другими словами – нужно просто решить частную конкретную задачу!
Одним из таких частных случаев является случай взаимодействия двух тел (или сводя все взаимодействия замкнутой механической системы к взаимодействию двух тел).
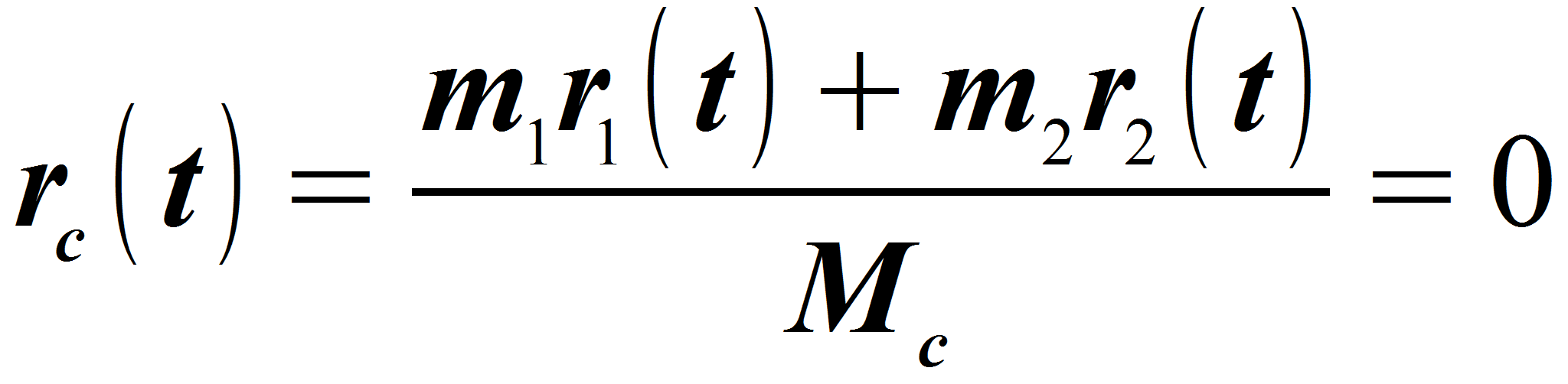
«Равно нулю» – при нулевых начальных условиях.
Но распространять одно частное решение на все случаи взаимодействий в любых изолированных механических системах, является грубой ошибкой.
От «частного» нельзя перейти к «общему».
1. ЦМ – это просто геометрическая координата. Результат математической функции.
2. Эта координата зависит: как от координат всех компонентов системы, так и от масс этих компонентов.
3. Изменяться с течением времени могут: как координаты компонентов системы, так и массы компонентов системы
4. ЦМ не обладает массой (см.п.1)
5. ЦМ не обладает импульсом (см.п.4)
6. Не обладает инерцией (см.п.4)
7. Функция координат ЦМ непрерывна и неразрывна Rc(t)=f(ri(t),mi(t))
8. Масса изолированной системы неизменна. Константа. Но эта константа есть функция от времени : Mc(t)=m1(t)+m2(t)=const
Функция координат ЦМ
может иметь такой вид: Rc(t)=const(t)
Так описывается безынерционное
перемещение.
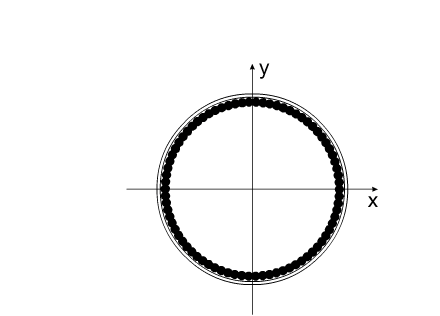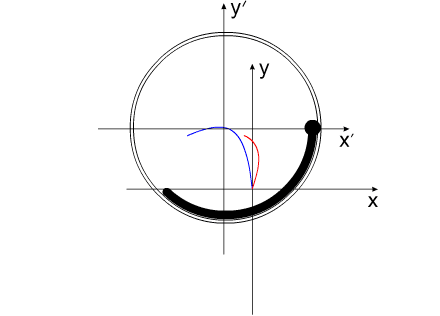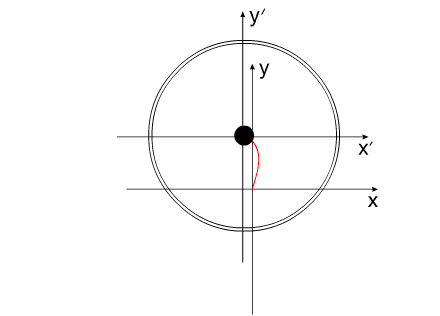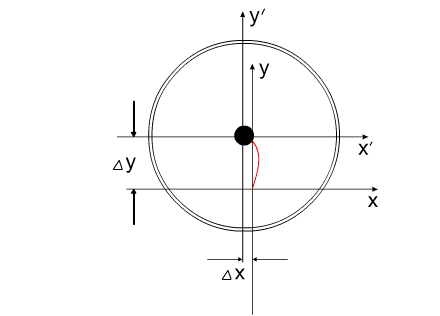
Варипенд (varipend) -
единственная механическая система, способная (принудительно)
изменять свое положение в пространстве без внешнего воздействия.
"Единственная" - примерно так же, как "единственен" гироскоп, демонстрирующий свойство "прецессия".
Перемещение варипенда можно назвать "линейной прецессией", поскольку это перемещение безынерционно, как и угловая прецессия гироскопа.
Можно сказать, что перемещение ЦМ механической системы "Varipend" - есть результат деформации этой механической системы.
Деформации, совершаемой с помощью внутренних взаимодействий.
Подробно, тщательно и очень наглядно, мой материал представлен на
сайте: http://varipend.narod.ru
Пожалуйста! Очень прошу! Посмотрите интернет-страницы!
«Аналогия
между вращательным и поступательным движениями» (http://varipend.narod.ru/analog)
«Нереактивное перемещение»
(http://varipend.narod.ru/not_reactive/)
Varipend. Варипенд (http://varipend.narod.ru)
Спасибо!
С наступающим Новым Годом!
--
С уважением,
Бутов Сергей Васильевич
238590, Россия,
Калининградская обл.,
г.Пионерский, ул.Октябрьская, д.5, кв.53
+7 981 4 53 55 89
+7 981 4 77 09 81
(8 401 2) 77 09 81
varipend@yandex.ru
http://varipend.narod.ru
Ответы
"редколлегии":
-------- Исходное сообщение --------
Тема: редакция ПММ Дата: Thu, 17 Jan 2013 15:55:20 +0400 От: ser <pmm.ipmnet@gmail.com> Кому: <varipend@yandex.ru>
Редколлегия что-то
решала? Или зав.редакцией и есть - редколлегия?
Ну как "не соответствуют"? Статьи не по механике?
Может быть, все же стоит читать то, что присылают? Может быть стоит
советоваться с членами редколлегии?
Зав.редакцией знает как выглядят "настоящие" статьи по механике?
-------- Исходное сообщение --------
Тема: varipend Дата: Wed, 23 Jan 2013 02:55:46 -0800 (PST) От: Yura Gupa <yuragupa@yahoo.com> Кому: varipend@yandex.ru <varipend@yandex.ru>
Глубокоуважаемый Сергей Васильевич!
Решением редколлегии от 25 декабря 2012 года Ваши статьи не приняты к
опубликованию в нашем журнале, так как в Ваших теоретических построениях
и выводах нарушены фундаментальные законы механики; по тем же
причинам редколлегия не принимает к рассмотрению труды по вечным
двигателям, телекинезу и т.п.
Редколлегия приносит Вам извинения за несанкционированный и неверный
ответ сотрудника редакции, не отражающий существа вопроса, в результате
чего Вы временно оказались введенным в заблуждение.
С уважением, Ю.П.Гупало, Ответственный секретарь редколлегии ПММ
Редколлегия
что-то решала? Или Ю.П.Гупало и есть - редколлегия?
Так значит, предыдущий ответ Натальи Олеговны был её собственной
инициативой? Порывом души, так сказать?
....
"Нарушены фундаментальные..."
Нарушены не "фундаментальные"! Нарушены наивные школьные
заблуждения,
которые совсем не стыдно декларировать секретарю редколлегии ПММ.
Может быть, все же стоит читать то, что присылают? Может быть стоит
советоваться с членами редколлегии?
Какой секретарь, такая и редколлегия?...
-------- Исходное сообщение --------
| From: | Мальцев Аркадий А. <maltsev@presidium.ras.ru> |
|---|---|
| To: | ' ButovSV' <varipend@yandex.ru> |
| Subject: | RE: Отказ редколлегии ПММ |
| Date: | Thu, 24 Jan 2013 11:03:13 +0400 |
Уважаемый Сергей Васильевич, по положению о журнале отказ редколлегии от публикации окончательный, и даже в суде обжалован быть не может. Есть другие журналы, обратитесь туда.
PS Дело в том, что благоденствие журнала зависит от тиража, а тираж зависит только от качества публикуемого материала. Редколлегия состоит из экспертов, но все равно каждая статья посылается и на внешний отзыв. Вероятность того, что будет отвергнута интересная (по профилю данного журнала) статья чрезвычайна мала, как показывает мой опыт (я уже четверть века работаю заместителем главного редактора журнала УМН) .
А.А.Мальцев, помощник президента
Суды бывают
разные. Есть такие, которые невозможно избежать...
Может быть, прежде, чем защищать отказ "редколлегии", необходимо
посмотреть "чему отказывают" и "кто отказывает"?
К отказу "редколлегии" я бы отнесся со всем уважением...
Но где же её взять, эту редколлегию?....
А может быть, взять, да и предложить создать настоящую
редколлегию? Сделать из ПММ "другой журнал"?
В любом случае, спасибо, Аркадий Анатольевич, за полезный совет!