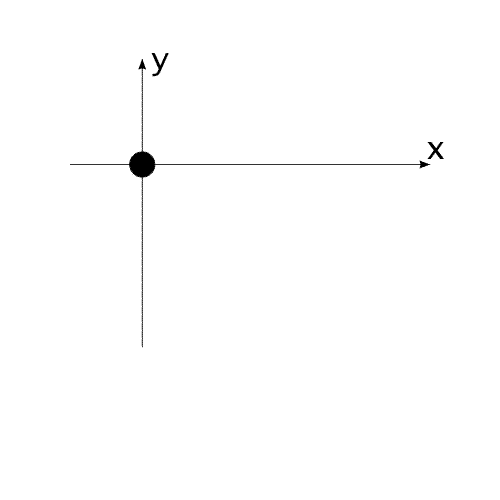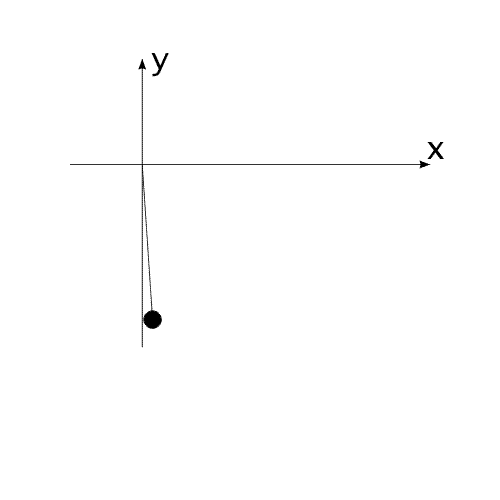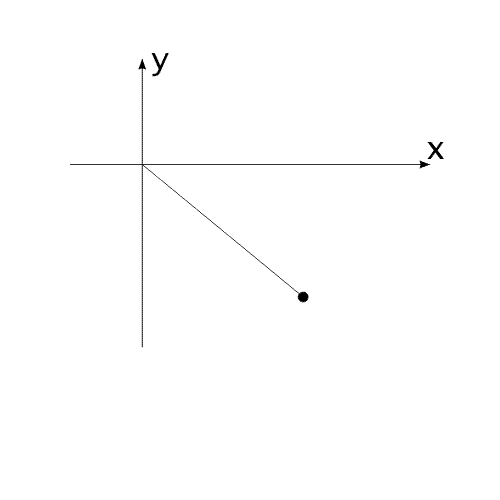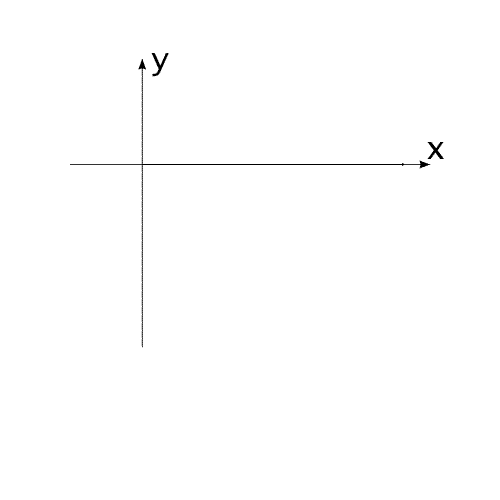|
О возможности перемещения замкнутой механической системы за счет внутренних сил.
Автор статьи не придумывает новые законы и ни в коем случае не пытается нарушить действующие. Возможно ли
переместить замкнутую механическую систему, на которую не действуют
внешние силы?
Следствия (2,3), собственно, и называют законом сохранения количества движения.
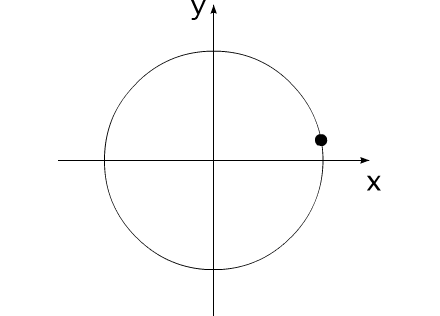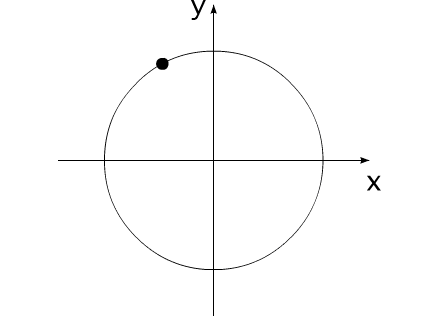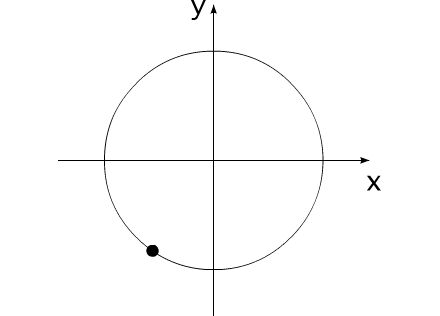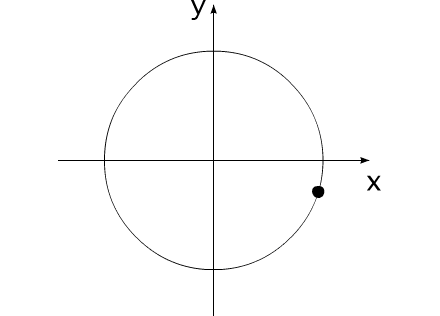
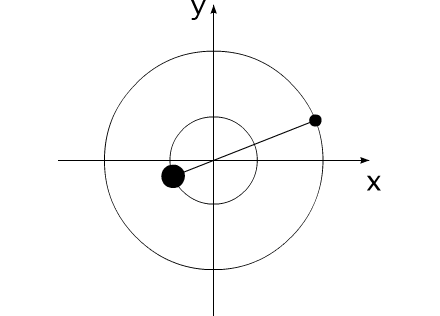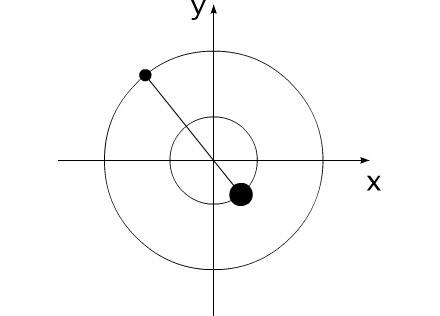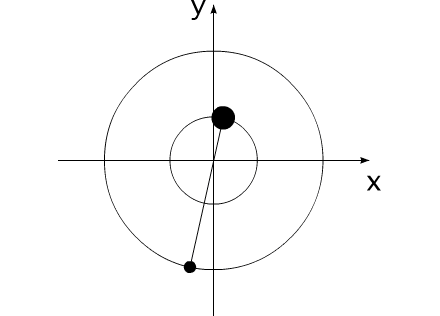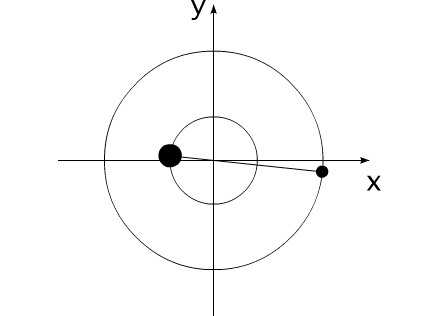
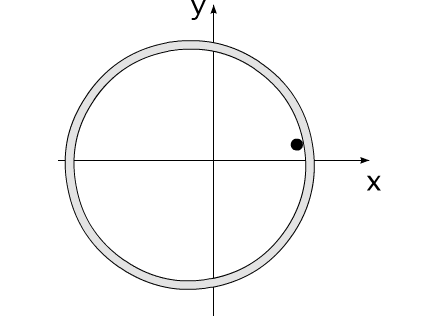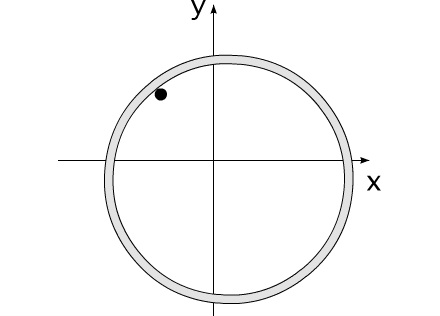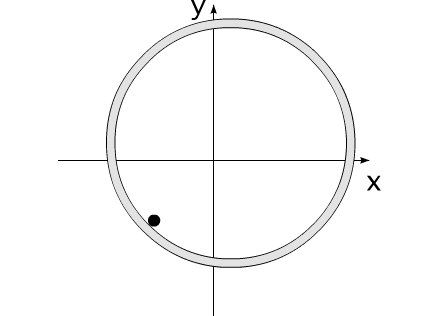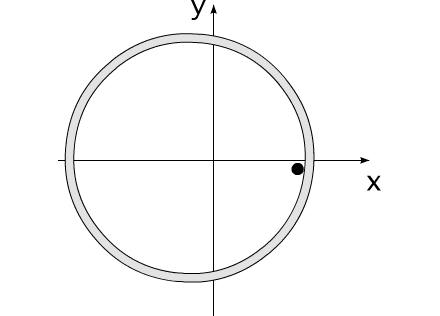
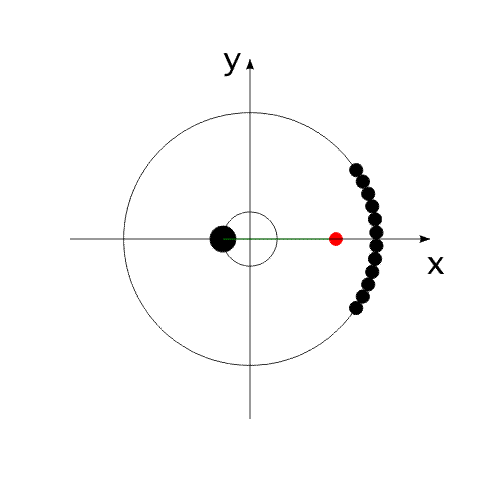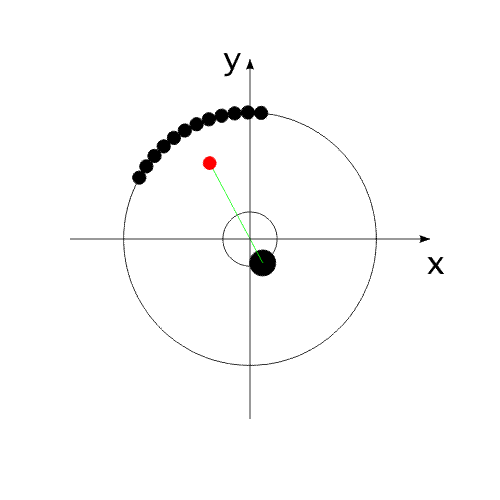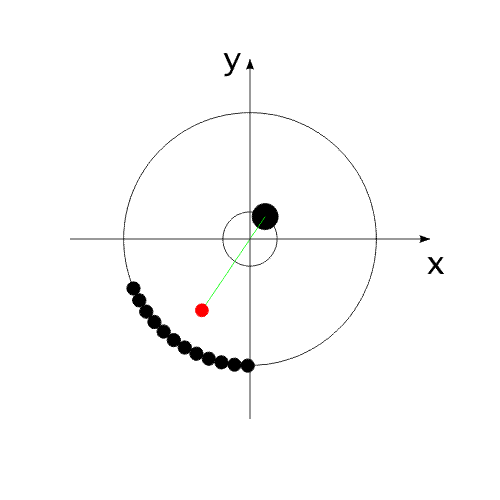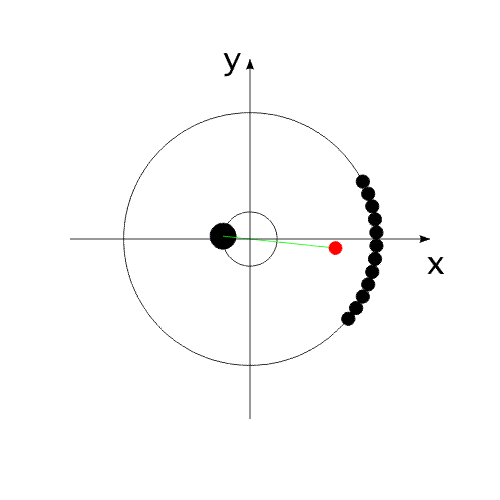
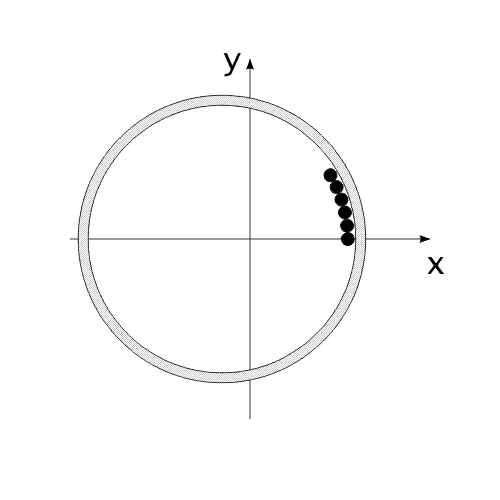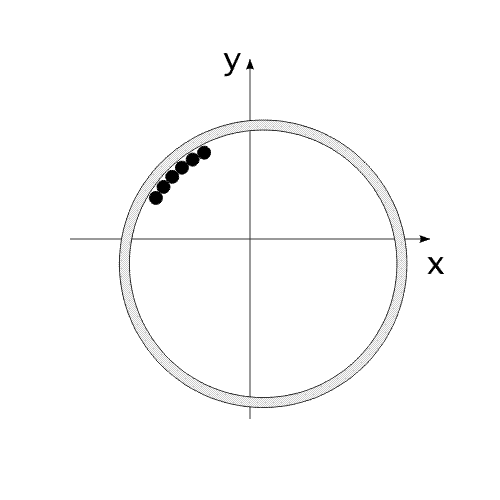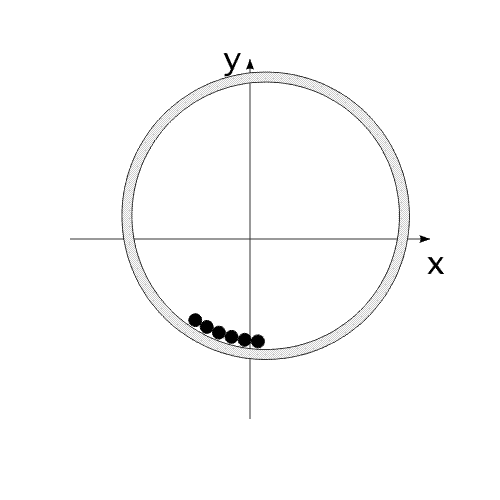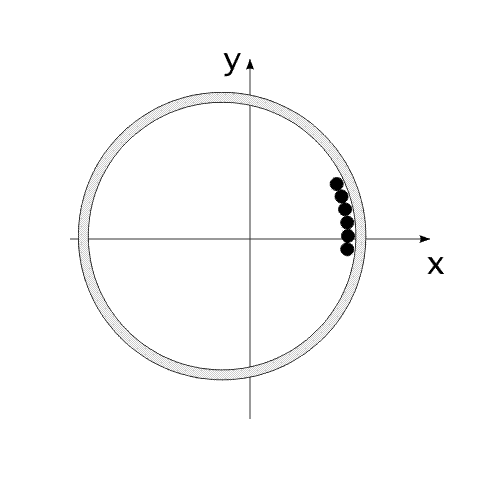
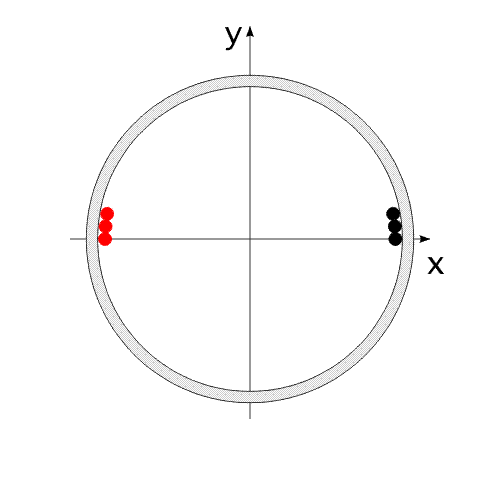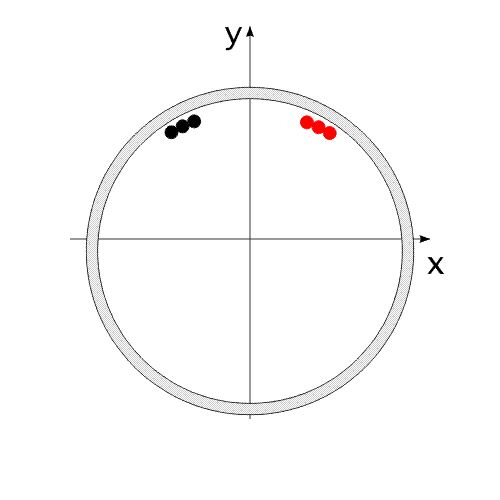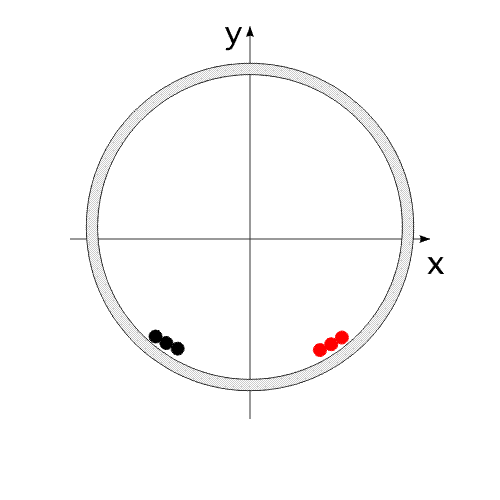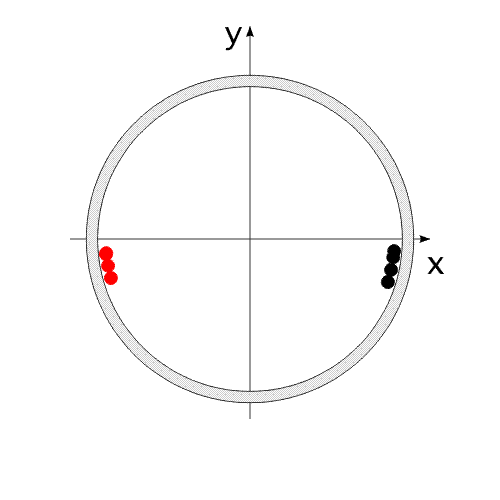
Закон сохранения количества движения нельзя нарушить. Невозможно! И его нельзя обойти. А нельзя ли его использовать для решения задачи, на первый взгляд, противоречащей этому закону?Предлагаю вашему вниманию следующую схему рассуждений: Показанное на Рис.1 перемещение тела не может быть осуществлено без участия в данном процессе другого тела.Поскольку количество движения тела, в проекции на оси координат, постоянно изменяется и отличается от нуля. Рис.1 Связанные между собой неразрывной и нерастяжимой связью тела могут перемещаться так, как изображено на Рис.2.При таком движении, тела будут двигаться по окружностям, радиусы которых обратно пропорциональны своим массам. Это - следствие закона сохранения импульса.В данном случае, суммарный импульс системы равен нулю. Рис.2 Вот как это выглядело бы в случае двух "реальных" объектов (Рис.3).Назовем одно из них "корпус", а другое - "рабочее тело", или "рабочее вещество". Рис.3 Если в относительном перемещении внутри (вокруг) корпуса примут участие два рабочих тела (имеющих одинаковые массы и скорости относительного перемещения) (Рис.4), то в таком случае, корпус не приобретет вращательное движение.Рис.4 В данном случае, суммарный импульс двух рабочих тел в проекции
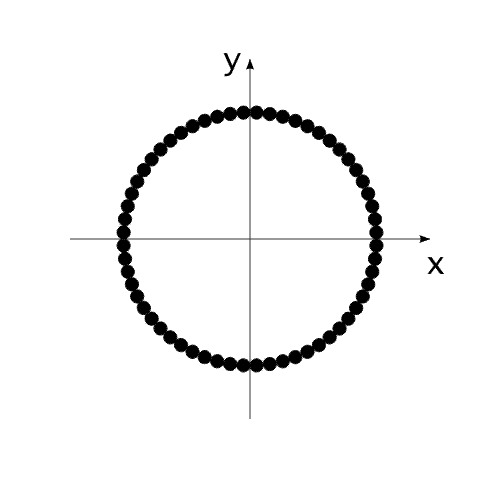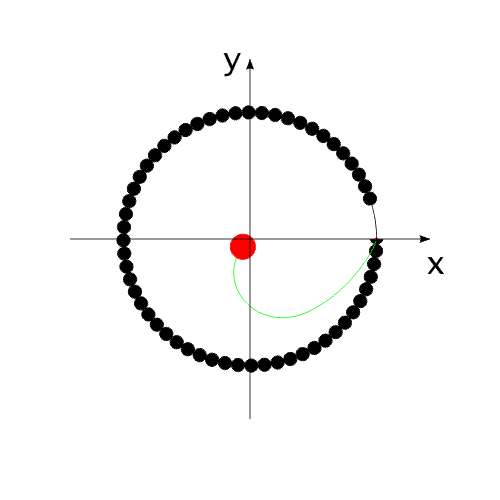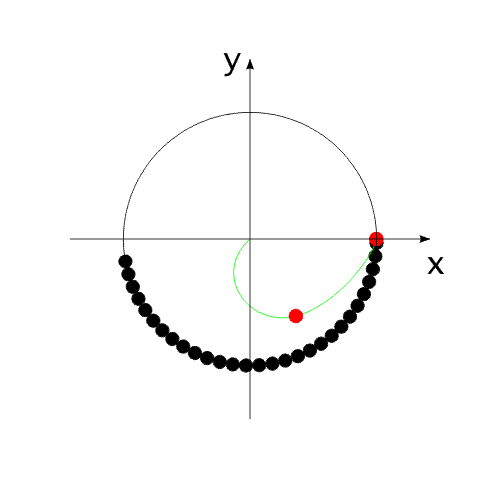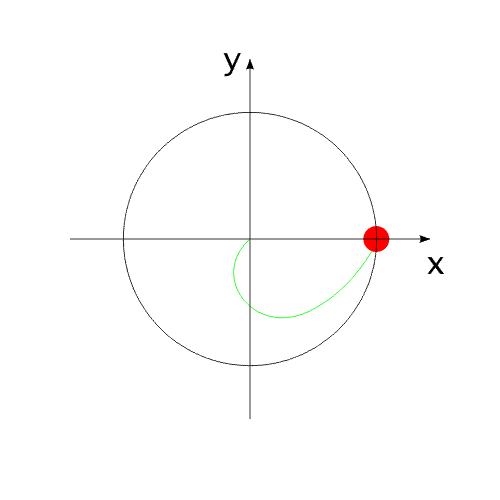
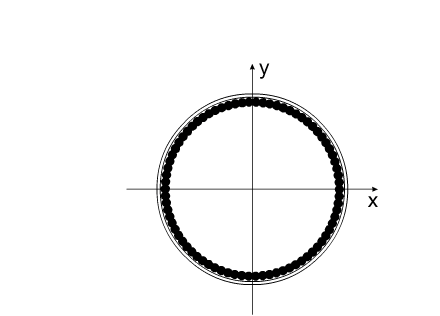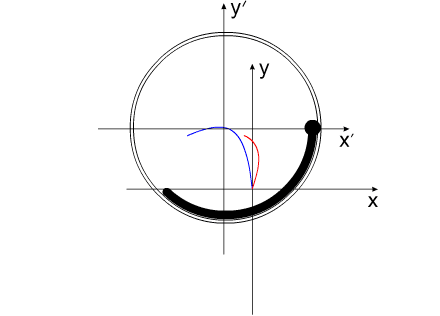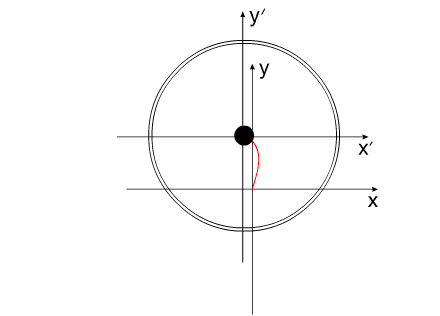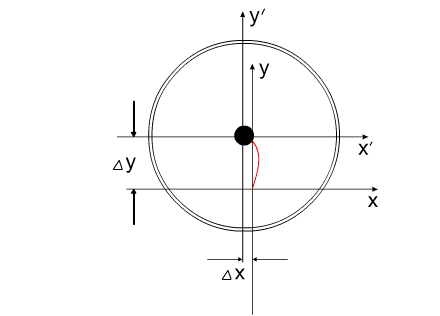
на ось Х равен нулю. Перемещение корпуса будет осуществляться вдоль одной оси "абсолютной", неподвижной системы координат. В системе координат, связанной с корпусом, рабочие тела перемещаются по окружности.В неподвижной системе координат, рабочие тела перемещаются по эллиптической траектории. Придать кинетическую энергию компонентам механической системы можно за счет преобразования других видов энергии, включенных в замкнутую систему.То есть, организовать относительные перемещения компонентов системы можно за счет внутренних сил. При этом центр масс всей системы всегда будет оставаться на месте, то есть не изменять своих координат (или двигаться прямолинейно и равномерно).Видоизменим систему, показанную на Рис.1 . Используем не "точечное" тело, а равномерно распределенную, на некотором участке траектории, рабочую массу (Рис.5). Рис.5 При равномерном относительном перемещении "корпус" и "рабочая масса" будут двигаться по окружностям, радиусы которых обратно пропорциональны своим массам (Рис.6). Под радиусом траектории рабочей массы необходимо подразумевать радиус траектории движения центра масс (ЦМ) рабочей массы (красная точка на рисунке).Рис.6 Вот как это выглядело бы для "реальной" системы тел.(Рис.7)Рис.7 Аналогично (Рис.4), можно использовать в системе несколько рабочих масс для уравновешивания момента импульса.(Рис.8)Опять таки, центр масс всей системы неподвижен. Рис.8 А что произойдет, если рабочая масса будет равномерно и неразрывно заполнять всю траекторию перемещения?(Рис.9)Да ничего! Центр масс рабочей массы совпадает с центром масс корпуса.Суммарный импульс распределенной рабочей массы в проекции на все оси координат равен нулю. Поэтому равен нулю и импульс корпуса.Центры масс компонентов системы не перемещаются относительно друг друга. Система стабильно неподвижна.При этом мы можем передать движущейся рабочей массе значительную кинетическую энергию. Рис.9 "Интересное" начинается, когда мы начинаем останавливать движущуюся рабочую массу в определенной точке траектории.(Рис.10) Останавливаем - это означает, в данном случае,-
последовательное "соединение" всех элементарных частиц рабочей массы с
корпусом. Рис.10 На анимированном рисунке красным цветом обозначен условный ЦМ рабочей массы. Зеленым - траектория перемещения ЦМ в своем относительном перемещении относительно "корпуса".Перемещение радиус-вектора ЦМ рабочей массы можно рассматривать, как перемещение маятника переменной массы и переменной длины. (В системе координат, связанной с корпусом.) (Рис.11) Рис.11 Вот тут и определилась интересная задача:рассчитать, как перемещаются компоненты системы? Расчеты привели к следующему результату (Рис.12). Рис.12 После завершения цикла остановки всей рабочей массы, ЦМ всей системы оказывается смещенным относительно своего начального положения. Система перемещается в полном соответствии с законом сохранения количества движения! Можно сказать иначе: Для того, чтобы выполнялся закон сохранения количества движения, центр масс данной механической системы обязан Первый расчет выполнен, исходя из закона сохранения импульса. Второй - с помощью уравнений Лагранжа II рода.Результаты совпадают. В решении этой задачи совершенно не рассматриваются внутренние взаимодействия компонентов системы.Никаких "соударений"! Никаких "сил инерции"!Только кинетическое и энергетическое состояние системы. На Рис.12 добавлен заключительный, дополнительный этап - сведение центров масс корпуса и рабочей массы в одну точку. Это необходимо для более наглядного представления всего цикла движения, с возможностью повторения этого цикла. Красная линия на рисунке обозначает траекторию перемещения ЦМ всей системы, синяя - ЦМ корпуса.Математические расчеты, описывающие данное предполагаемое явление, вы можете посмотреть по адресу: https://varipend.narod.ru С.Бутов23 декабря 2006 Защищено законодательством Российской Федерации по
авторским правам. |
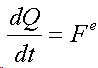
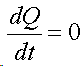
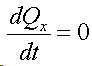
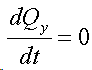
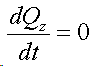
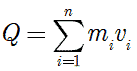остаётся постоянной. 
